题目内容
20．如果关于x的一元二次方程x2+4x-m=0没有实数根，那么m的取值范围是m＜-4．分析 根据关于x的一元二次方程x2+4x-m=0没有实数根，得出△=16-4（-m）＜0，从而求出m的取值范围．
解答 解：∵一元二次方程x2+4x-m=0没有实数根，
∴△=16-4（-m）＜0，
∴m＜-4，
故答案为m＜-4．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
阅读快车系列答案
相关题目
11．若一组数据3，x，4，5，6的众数为6，则这组数据的中位数为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
15．如果一个正多边形的中心角为72°，那么这个多边形的边数是（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
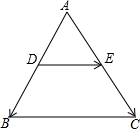如图，已知在△ABC中，D、E分别是边AB、边AC的中点，$\overrightarrow{AB}$=$\overrightarrow{m}$，$\overrightarrow{AC}$=$\overrightarrow{n}$，那么向量$\overrightarrow{DE}$用向量$\overrightarrow{m}$，$\overrightarrow{n}$表示为$\frac{1}{2}$$\overrightarrow{n}$-$\frac{1}{2}$$\overrightarrow{m}$．
12．下列计算正确的是（ ）
| A． | a2+a2=a4 | B． | a2•a3=a6 | C． | （-a2）2=a4 | D． | （a+1）2=a2+1 |