��Ŀ����
20���������x��һԪ���η���ax2+bx+c=0������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ���������̡�������˵�����ٷ���x2-2x-8=0�DZ������̣�
������x-2����mx+n��=0�DZ������̣���m=-n��m=-$\frac{1}{4}$n��
��������ax2+bx+c=0�DZ������̣�����������M��2+t��s����N��4-t��s������������y=ax2+bx+c�ϣ���ax2+bx+c=0��һ����Ϊ2��
���У���ȷ˵���ĸ����ǣ�������
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ��ͨ���ⷽ�̵õ��÷��̵ĸ�����ϡ��������̡��Ķ�������жϣ�
��ͨ���ⷽ����÷��̵������⣬��ϡ��������̡��Ķ�������m��n��������ϵ��
���ɷ���ax2+bx+c=0�DZ������̣��õ�x1=2x2������������M��2+t��s����N��4-t��s������������y=ax2+bx+c�ϣ�ͨ�������߶Գ������x1��ֵ��
��� �⣺����x2-2x-8=0����
��x-4����x+2��=0��
���x1=4��x2=-2��
��x1��2x2����x2��2x1��
���x2-2x-8=0���DZ������̣�
�ʢٴ���
�ڽⷽ�̣�x-2����mx+n��=0����
x1=2��x2=-$\frac{n}{m}$��
�ߣ�x-2����mx+n��=0�DZ������̣�
��2=-$\frac{2n}{m}$��4=-$\frac{n}{m}$��
��m=-n��m=-$\frac{1}{4}$n��
�ʢ���ȷ��
�߷���ax2+bx+c=0�DZ������̣�
����x1=2x2��
����������M��2+t��s����N��4-t��s������������y=ax2+bx+c�ϣ�
�������ߵĶԳ���x=$\frac{2+t+4-t}{2}$=3��
��x1+x2=6��
��x1+2x1=6��
��x1=2��
�ʢ���ȷ��
������������ȷ�ĸ�����2����
��ѡ��C��
���� ���⿼���˸���ϵ���Ĺ�ϵ�������б�ʽ������������ͼ���ϵ���������������κ���ͼ���ϵ��������������ȷ�����⡰�������̡��Ķ����ǽ���Ĺؼ���

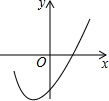 ��ͼ���κ���y=ax2+bx+c�IJ���ͼ�������꣨-1��-3.2������ͼ���֪����x�ķ���ax2+bx+c=0������x1=1.3��x2=-3.3��
��ͼ���κ���y=ax2+bx+c�IJ���ͼ�������꣨-1��-3.2������ͼ���֪����x�ķ���ax2+bx+c=0������x1=1.3��x2=-3.3��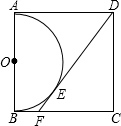 ������ABCD��һ��ABΪֱ����������������ԲO������D�������Բ�����߽�BC�ڵ�F��EΪ�е㣬BF=1����������ABCD�ı߳���
������ABCD��һ��ABΪֱ����������������ԲO������D�������Բ�����߽�BC�ڵ�F��EΪ�е㣬BF=1����������ABCD�ı߳���