题目内容
5.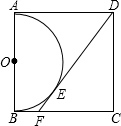 正方形ABCD的一边AB为直径在正方形内作半圆O,过点D作这个半圆的切线交BC于点F,E为切点,BF=1,求正方形ABCD的边长.
正方形ABCD的一边AB为直径在正方形内作半圆O,过点D作这个半圆的切线交BC于点F,E为切点,BF=1,求正方形ABCD的边长.
分析 设正方形ABCD的边长为a,先判断AD和CB为半圆O的切线,则根据切线长定理得到CE=FB=1,DE=DA=a,所以CF=CB-BF=a-1,DF=EF+DE=a+1,然后在Rt△CDF中根据勾股定理得到(a-1)2+a2=(a+1)2,再解方程即可得到正方形ABCD的边长.
解答 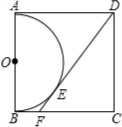 解:设正方形ABCD的边长为a,
解:设正方形ABCD的边长为a,
∵AB为半圆O的直径,
而DA⊥AB,CB⊥AB,
∴AD和CB为半圆O的切线,
∵DF为半圆O的切线,
∴CE=FB=1,DE=DA=a,
∴CF=CB-BF=a-1,DF=EF+DE=a+1,
在Rt△CDF中,∵CF2+CD2=DF2,
∴(a-1)2+a2=(a+1)2,解得a1=0(舍去),a2=4,
即正方形ABCD的边长为4.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了正方形的性质和切线长定理.

练习册系列答案
相关题目
10.如果|x|=3,则|x+1|的值是( )
| A. | 4 | B. | 2 | C. | 4或2 | D. | 以上都不对 |
 在△ABC中,∠B=50°,∠C=60°,AD是高,AE是角平分线,求∠EAD的度数.
在△ABC中,∠B=50°,∠C=60°,AD是高,AE是角平分线,求∠EAD的度数.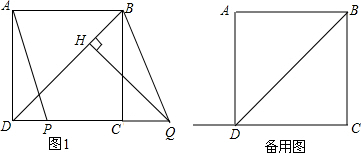
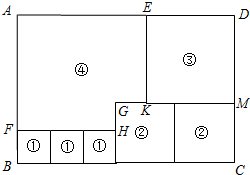 如图,用3个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个长方形ABCD.若GH=2cm,GK=2cm,设BF=x cm.
如图,用3个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个长方形ABCD.若GH=2cm,GK=2cm,设BF=x cm.