题目内容
16.(1)如图①,已知:△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥m于D,CE⊥m于E,求证:DE=BD+CE;(2)拓展:如图②,将(1)中的条件改为:△ABC中,AB=AC,D、A、E三点都在直线m上,并且∠BDA=∠AEC=∠BAC=α,α为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请证明;若不成立,请说明理由;
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,直线m与BC的延长线交于点F,若BC=2CF,△ABC的面积是12,求△ABD与△CEF的面积之和.
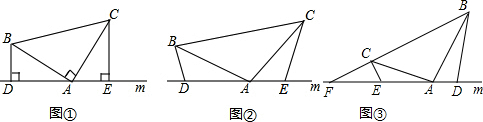
分析 (1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,由AAS证得△ADB≌△CEA,则AE=BD,AD=CE,即可得出结论;
(2)由∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,由AAS证得△ADB≌△CEA即可得出答案;
(3)由∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,∴∠CAE=∠ABD,得出∠CAE=∠ABD,由AAS证得△ADB≌△CEA,得出S△ABD=S△CEA,再由不同底等高的两个三角形的面积之比等于底的比,得出S△ACF即可得出结果.
解答 (1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)解:结论DE=BD+CE成立;理由如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(3)解:∵∠BAD>∠CAE,∠BDA=∠AEC=∠BAC,
∴∠CAE=∠ABD,
在△ABD和△CEA中,$\left\{\begin{array}{l}{∠ABD=∠CAE}\\{∠BDA=∠CEA}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CEA(AAS),
∴S△ABD=S△CEA,
设△ABC的底边BC上的高为h,则△ACF的底边CF上的高为h,
∴S△ABC=$\frac{1}{2}$BC•h=12,S△ACF=$\frac{1}{2}$CF•h,
∵BC=2CF,
∴S△ACF=6,
∵S△ACF=S△CEF+S△CEA=S△CEF+S△ABD=6,
∴△ABD与△CEF的面积之和为6.
点评 本题考查了全等三角形的判定与性质及不同底等高的两个三角形的面积之比等于底的比,结合题目所给条件,得出∠CAE=∠ABD是解决问题的关键.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
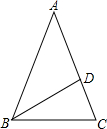 如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.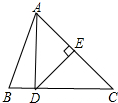 如图,△ABC中,∠B=80°,DE是AC的垂直平分线,且∠ABD:∠DAC=1:2,则∠C的度数为40°.
如图,△ABC中,∠B=80°,DE是AC的垂直平分线,且∠ABD:∠DAC=1:2,则∠C的度数为40°.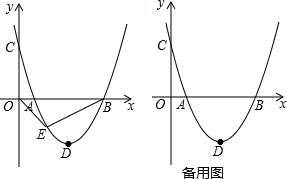
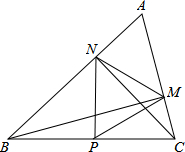 如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)
如图,在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AB于点N.P为BC边的中点,连接PM、PN,则下列结论:①PM=PN;②$\frac{AM}{AB}=\frac{AN}{AC}$;③△PMN为等边三角形;④当△ABC=45°时,BN=PC,其中正确的是①②③.(把所有正确结论的序号都选上)