题目内容
1.如图,抛物线经过点A(1,0),B(5,0),C(0,$\frac{10}{3}$)三点,顶点为D,设点E(x,y)是抛物线上一动点,且在x轴下方.(1)求抛物线的解析式;
(2)当点E(x,y)运动时,试求三角形OEB的面积S与x之间的函数关系式,并求出面积S的最大值?
(3)在y轴上确定一点M,使点M到D、B两点距离之和d=MD+MB最小,求点M的坐标.
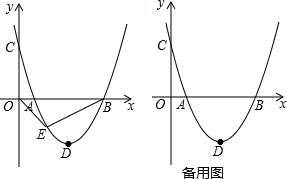
分析 (1)设出解析式,由待定系数法可得出结论;
(2)点E在抛物线上,用x去表示y,结合三角形面积公式即可得出三角形OEB的面积S与x之间的函数关系式,再由E点在x轴下方,得出1≤x≤5,将三角形OEB的面积S与x之间的函数关系式配方,即可得出最值;
(3)找出D点关于y轴对称的对称点D′,结合三角形内两边之和大于第三边,即可确定当MD+MB最小时M点的坐标.
解答 解:(1)设抛物线解析式为y=ax2+bx+c,则
$\left\{\begin{array}{l}{0=a+b+c}\\{0=25a+5b+c}\\{\frac{10}{3}=c}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-4}\\{c=\frac{10}{3}}\end{array}\right.$.
故抛物线解析式为y=$\frac{2}{3}$x2-4x+$\frac{10}{3}$.
(2)过点E作EF⊥x轴,垂足为点F,如图1所示.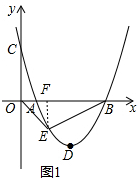
E点坐标为(x,$\frac{2}{3}$x2-4x+$\frac{10}{3}$),F点的坐标为(x,0),
∴EF=0-($\frac{2}{3}$x2-4x+$\frac{10}{3}$)=-$\frac{2}{3}$x2+4x-$\frac{10}{3}$.
∵点E(x,y)是抛物线上一动点,且在x轴下方,
∴1≤x≤5.
三角形OEB的面积S=$\frac{1}{2}$OB•EF=$\frac{1}{2}$×5×(-$\frac{2}{3}$x2+4x-$\frac{10}{3}$)=-$\frac{5}{3}$(x-3)2+$\frac{20}{3}$(1≤x≤5).
当x=3时,S有最大值$\frac{20}{3}$.
(3)作点D关于y轴的对称点D′,连接BD′,如图2所示.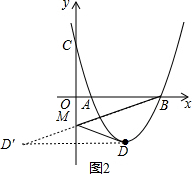
∵抛物线解析式为y=$\frac{2}{3}$x2-4x+$\frac{10}{3}$=$\frac{2}{3}$(x-3)2-$\frac{8}{3}$,
∴D点的坐标为(3,-$\frac{8}{3}$),
∴D′点的坐标为(-3,-$\frac{8}{3}$).
由对称的特性可知,MD=MD′,
∴MB+MD=MB+MD′,
当B、M、D′三点共线时,MB+MD′最小.
设直线BD′的解析式为y=kx+b,则
$\left\{\begin{array}{l}{0=5k+b}\\{-\frac{8}{3}=-3k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-\frac{5}{3}}\end{array}\right.$,
∴直线BD′的解析式为y=$\frac{1}{3}$x-$\frac{5}{3}$.
当x=0时,y=-$\frac{5}{3}$,
∴点M的坐标为(0,-$\frac{5}{3}$).
点评 本题考查了二次函数的运用、待定系数法求二次函数解析式、点的对称以及三角形边的关系,解题的关键是:(1)能够熟练运用待定系数法求解析式;(2)利用三角形面积公式找出三角形面积的解析式,再去配方求最值;(3)先找对称点,再结合三角形内两边之和大于第三边确定点M的位置.本题属于中档题,难度不大,失分点在于(2)中部分同学会忘记求x的取值范围;(3)中不会用找对称点借助三角形边的关系确定M点的位置.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案| A. | 全等三角形的对应角相等 | B. | 对于实数a、b、c,若a>b,则ac2>bc2 | ||
| C. | 互补的两个角不可能都是锐角 | D. | 若直线a、b、c满足a∥b,b∥c,则a∥c |
| A. | a-9>b-9 | B. | 3b<3a | C. | -2a>-2b | D. | $\frac{a}{5}$>$\frac{b}{5}$ |
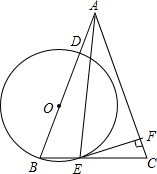 如图,在△ABC中,AB=AC,tanC=3.点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3.点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.