题目内容
4.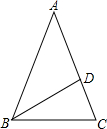 如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.
如图,在△ABC中,AB=AC,∠A=36°,点D是AC上一点,BD平分∠ABC.(1)求$\frac{AC}{BC}$的值;
(2)将线段AD绕点A逆时针旋转α(0°<α<180°),得到线段AE,在旋转的过程中,是否存在CE∥AB?若存在,求出相应的旋转角α;若不存在,请说明理由.
分析 (1)设BC=1,AB=x,由△BDC∽△ABC得$\frac{AB-BC}{BC}=\frac{BC}{AB}$,列出方程求出x即可解决.
(2)存在.以A为圆心,AD为半径画圆,作CM∥AB,交⊙A于M、N两点,M、N、即为所的E点,由AD=AM=AN=BC,AB∥CM,得四边形ANCN是平行四边形,四边形ABCM是等腰梯形,由此即可解决旋转角的大小.
解答 (1)解:∵AB=AC,∠A=36°,∠C=∠BDC=72°,
∴AD=BD=BC,
∴△BDC∽△ABC,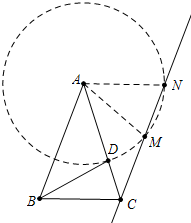
∴$\frac{CD}{BC}=\frac{BC}{AB}$,$\frac{AC-AD}{BC}=\frac{BC}{AB}$
即$\frac{AB-BC}{BC}=\frac{BC}{AB}$,设BC=1,AB=x,得x-1=$\frac{1}{x}$解得x=$\frac{\sqrt{5}+1}{2}$(或$\frac{-\sqrt{5}+1}{2}$舍弃),
∴$\frac{AB}{BC}$=$\frac{\sqrt{5}+1}{2}$.
(2)存在,理由如下:
证明:如图,以A为圆心,AD为半径画圆,作CM∥AB,交⊙A于M、N两点,M、N、即为所的E点.
∵AD=AM=AN=BC,AB∥CM,
∴四边形ANCN是平行四边形,四边形ABCM是等腰梯形,
∴∠NAD=∠ACB=72°,∠MAB=∠ABC=72°,∠MAD=∠MAB-∠BAC=72°-36°=36°,
∴旋转角为36°或72°.
点评 本题考查相似三角形的判定和性质、等腰三角形的性质、以及平行四边形、等腰梯形的判定和性质,解题的关键是利用相似三角形列出比例式,转化为方程解决.

练习册系列答案
相关题目
14.关于抛物线y=x2-4x-5,下列结论不正确的是( )
| A. | 抛物线开口向上 | B. | 抛物线的对称轴是x=2 | ||
| C. | 当x=2时,y的最大值为-9 | D. | 抛物线与x轴的交点为(-1,0),(5,0) |
15.下列各式中,不是同类项的是( )
| A. | $\frac{1}{2}$x2y和$\frac{1}{3}$x2y | B. | -ab和ba | C. | -1和3 | D. | $\frac{2}{5}$x2y和$\frac{5}{2}$xy3 |
14.如图图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
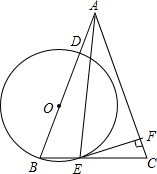 如图,在△ABC中,AB=AC,tanC=3.点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.
如图,在△ABC中,AB=AC,tanC=3.点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F,且BD=2EF.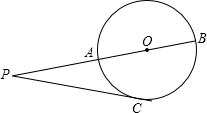 已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P、Q两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=$\frac{7}{8}$cm.
已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P、Q两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=$\frac{7}{8}$cm.
 如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
如图,AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.