题目内容
17.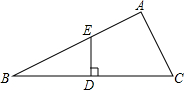 如图,已知在△ABC中,∠A=90°,D是BC中点,且DE⊥BC于D,交AB于E,求证:BE2-EA2=AC2.
如图,已知在△ABC中,∠A=90°,D是BC中点,且DE⊥BC于D,交AB于E,求证:BE2-EA2=AC2.
分析 连接CE,根据线段垂直平分线性质求出BE=CE,根据勾股定理得出CE2-EA2=AC2,代入求出即可.
解答 证明:连接CE,
∵D是BC中点,DE⊥BC,
∴BE=CE,
∵∠A=90°,
∴CE2-EA2=AC2,
∴BE2-EA2=AC2.
点评 本题考查了勾股定理,线段垂直平分线性质的应用,解此题的关键是能正确作出辅助线,注意:线段垂直平分线上的点到线段两个端点的距离相等,直角三角形的两直角边的平方和等于斜边的平方.

练习册系列答案
相关题目
12.工地调来72人参加挖土和运土,已知3人挖出的土1人恰好能全部运走,怎样调动劳动力才能使挖出的土能及时运走.解决此问题,可设派x人挖土,其它的人运土,可列方程( )
| A. | $\frac{72-x}{x}$=$\frac{1}{3}$ | B. | 72-x=3x | C. | x+3x=72 | D. | $\frac{x}{72-x}$=$\frac{1}{3}$ |
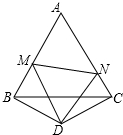 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120度.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.
如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120度.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN. 如图,在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
如图,在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):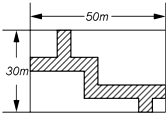 如图所示,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为2米,其他部分均种植花草,则种植花草的面积是1344米2.
如图所示,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为2米,其他部分均种植花草,则种植花草的面积是1344米2.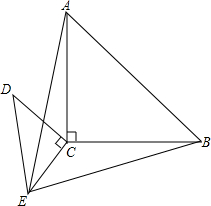 把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC
把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC