题目内容
4.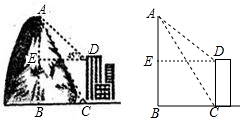 某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)
某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)
分析 过D作AB的垂线,设垂足为E.在Rt△ABC中,可用AB表示出BC的长,进而可在Rt△ADE中,表示出AE的长;根据BE=AB-AE=12,即可求出山高AB的长度.
解答  解:过D作DE⊥AB于E,则DE∥BC.
解:过D作DE⊥AB于E,则DE∥BC.
设AB=h米.
在Rt△ABC中,BC=h•cot60°=h•tan30°=$\frac{\sqrt{3}}{3}$h.
在Rt△AED中,AE=DEtan45°=$\frac{\sqrt{3}}{3}$h.
又∵AB-AE=BE=CD=12,
∴h-$\frac{\sqrt{3}}{3}$h=12,
解得h=$\frac{12}{1-\frac{\sqrt{3}}{3}}$=$\frac{36}{3-\sqrt{3}}$=18+6$\sqrt{3}$.
答:山高AB是(18+6$\sqrt{3}$)米.
点评 考查了解直角三角形的应用-仰角俯角问题,解直角梯形可以通过作高线转化为解直角三角形和矩形的问题.

练习册系列答案
相关题目
15.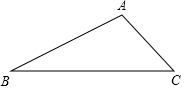 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
(1)用尺规作∠BAC的角平分线AE;
(2)用三角板作AC边上的高BD;
(3)用尺规作AC边上的垂直平分线MN.
 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)(1)用尺规作∠BAC的角平分线AE;
(2)用三角板作AC边上的高BD;
(3)用尺规作AC边上的垂直平分线MN.
9.下列各式结果为负数的是( )
| A. | -(-5) | B. | -|-3| | C. | (-2)6 | D. | |2-6| |
13. 如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
 如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,黑色部分的 图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形的概率是( )| A. | $\frac{3}{13}$ | B. | $\frac{4}{13}$ | C. | $\frac{5}{13}$ | D. | $\frac{6}{13}$ |
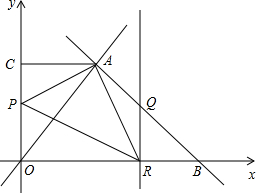 如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.
如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.