题目内容
4.丽水某公司将“丽水山耕”农副产品运往杭州市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:| v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
| t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(2)汽车上午7:30从丽水出发,能否在上午10:00之前到达杭州市场?请说明理由;
(3)若汽车到达杭州市场的行驶时间t满足3.5≤t≤4,求平均速度v的取值范围.
分析 (1)根据表格中数据,可知v是t的反比例函数,设v=$\frac{k}{t}$,利用待定系数法求出k即可;
(2)根据时间t=2.5,求出速度,即可判断;
(3)根据自变量的取值范围,求出函数值的取值范围即可;
解答 解:(1)根据表格中数据,可知v=$\frac{k}{t}$,
∵v=75时,t=4,
∴k=75×4=300,
∴v=$\frac{300}{t}$.
(2)∵10-7.5=2.5,
∴t=2.5时,v=$\frac{300}{2.5}$=120>100,
∴汽车上午7:30从丽水出发,不能在上午10:00之前到达杭州市场.
(3)∵3.5≤t≤4,
∴75≤v≤$\frac{600}{7}$,
答:平均速度v的取值范围是75≤v≤$\frac{600}{7}$.
点评 本题考查反比例函数的应用,待定系数法等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
 如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
如图,MN是⊙O的直径,MN=8,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
15. 如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{8}{x}$(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=EC,四边形ODBE的面积为( )| A. | 6 | B. | 7 | C. | 8 | D. | 12 |
12.为了考察甲、乙两种成熟期小麦的株高长势情况,现从中随机抽取6株,并测得它们的株高(单位:cm)如表所示:
(1)请分别计算表内两组数据的方差,并借此比较哪种小麦的株高长势比较整齐?
(2)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
| 甲 | 63 | 66 | 63 | 61 | 64 | 61 |
| 乙 | 63 | 65 | 60 | 63 | 64 | 63 |
(2)现将进行两种小麦优良品种杂交实验,需从表内的甲、乙两种小麦中,各随机抽取一株进行配对,以预估整体配对状况,请你用列表法或画树状图的方法,求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率.
19.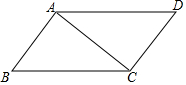 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
9.对于二次函数y=-(x-1)2+2的图象与性质,下列说法正确的是( )
| A. | 对称轴是直线x=1,最小值是2 | B. | 对称轴是直线x=1,最大值是2 | ||
| C. | 对称轴是直线x=-1,最小值是2 | D. | 对称轴是直线x=-1,最大值是2 |
16.据调查,某班20位女同学所穿鞋子的尺码如表所示,则鞋子尺码的众数和中位数分别是( )
| 尺码(码) | 34 | 35 | 36 | 37 | 38 |
| 人数 | 2 | 5 | 10 | 2 | 1 |
| A. | 35码,35码 | B. | 35码,36码 | C. | 36码,35码 | D. | 36码,36码 |
13.使代数式$\frac{1}{\sqrt{x+3}}$+$\sqrt{4-3x}$有意义的整数x有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
16.已知a<b,下列四个不等式中正确的是( )
| A. | 3a>3b | B. | -a<-b | C. | a+3<b+3 | D. | a-6>b-6 |