Question

9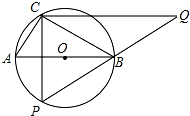．如图，Rt△ABC中，AB=10，AC：BC=3：4，以斜边AB为直径作⊙O，动点P在直径下方的半圆AB上运动（不与A、B重合），过点C作CQ⊥CP，与PB的延长线交于点Q．
（1）当CP⊥AB时，求CQ的长；
（2）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．

Answer 1

分析 （1）根据Rt△ABC中，AB=10，AC：BC=3：4，求得AC=6，BC=8，再根据CP⊥AB，得到CP=2CM，据此求得CP的长，再根据△CAB∽△CPQ，得到$\frac{CQ}{CB}$=$\frac{CP}{CA}$，进而得出CQ=$\frac{CB•CP}{CA}$=$\frac{64}{5}$；
（2）由（1）可知，CQ=$\frac{CB•CP}{CA}$=$\frac{4}{3}$CP，根据当CP取最大值是CQ有最大值，得到当CP为直径时，即点P运动到CP经过圆心O时，CQ取到最大值为$\frac{40}{3}$．

解答 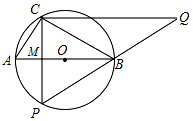解：（1）∵Rt△ABC中，AB=10，AC：BC=3：4，
∴AC=6，BC=8，
设CP交AB于M，
∵CP⊥AB，
∴CP=2CM=2×$\frac{24}{5}$=$\frac{48}{5}$，
∵∠A=∠P，∠ACB=∠PCQ=90°，
∴△CAB∽△CPQ，
∴$\frac{CQ}{CB}$=$\frac{CP}{CA}$，
∴CQ=$\frac{CB•CP}{CA}$=$\frac{64}{5}$；

（2）由（1）可知，CQ=$\frac{CB•CP}{CA}$=$\frac{4}{3}$CP，
∴当CP取最大值是CQ有最大值，
∴当CP为直径时，即点P运动到CP经过圆心O时，CQ取到最大值为$\frac{4}{3}$×10=$\frac{40}{3}$．

点评 本题主要考查了相似三角形的判定与性质，圆周角定理的运用，解决问题的关键是根据相似三角形的对应边成比例，列出比例式进行计算求解．