题目内容
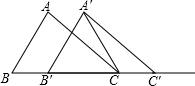如图，在△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移2个单位后，得到△A′B′C′，连接A′C，则△A′B′C的周长为考点：平移的性质
专题：
分析：根据平移性质，判定△A′B′C为等边三角形，然后求解．
解答：解：由题意，得BB′=2，
∴B′C=BC-BB′=4．
由平移性质，可知A′B′=AB=4，∠A′B′C=∠ABC=60°，
∴A′B′=B′C，且∠A′B′C=60°，
∴△A′B′C为等边三角形，
∴△A′B′C的周长=3A′B′=12．
故答案为：12．
∴B′C=BC-BB′=4．
由平移性质，可知A′B′=AB=4，∠A′B′C=∠ABC=60°，
∴A′B′=B′C，且∠A′B′C=60°，
∴△A′B′C为等边三角形，
∴△A′B′C的周长=3A′B′=12．
故答案为：12．
点评：本题考查的是平移的性质，熟知图形平移后新图形与原图形的形状和大小完全相同是解答此题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
如图，已知：△ABC中，AB=AC，M是BC的中点，D、E分别是AB、AC边上的点，且BD=CE．求证：MD=ME．
如图，一艘轮船以30海里/小时的速度由西向东航行，途中接到台风警报，台风中心正以60海里/小时的速度由南向北移动，距台风中心20海里的圆形区域（包括边界）都属于台风区，当轮船到A处时，测得台风中心移到位于点A正南方向的B处，且AB=40海里．
如图，点G是△ABC的重心，CG的延长线交AB于点D，GA=10，GC=8，GB=6，将△ADG绕点D顺时针方向旋转180°得到△BDE，则△EBC的面积为
如图，点A、B、C都在圆O上，如果∠AOB+∠ACB=84°，那么∠ACB的大小是
如图，圆锥的表面展开图由一扇形和一个圆组成，已知圆的面积为100π，扇形的圆心角为120°，这个扇形的面积为