题目内容
 如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为
如图,点G是△ABC的重心,CG的延长线交AB于点D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积为考点:旋转的性质
专题:
分析:根据点G是△ABC的重心,CG的延长线交AB于D,GA=10,GC=8,GB=6,将△ADG绕点D顺时针方向旋转180°得到△BDE,得出DG=DE=4,以及BE=10,即可得出△EBG的面积,进而得出答案.
解答:解:∵点G是△ABC的重心,CG的延长线交AB于D,GC=8,
∴DE=4,
∵将△ADG绕点D顺时针方向旋转180°得到△BDE,
∴DG=DE=4,AG=BE=10,∵BG=6,
∴△BGE是直角三角形,
∴△BGE的面积为:
×6×8=24,
∵∠BGE=90°,
∴∠BGC=90°,
∴△BGC的面积为:
×6×8=24,
∴△EBC的面积为:48.
故答案为:48.
∴DE=4,
∵将△ADG绕点D顺时针方向旋转180°得到△BDE,
∴DG=DE=4,AG=BE=10,∵BG=6,
∴△BGE是直角三角形,
∴△BGE的面积为:
| 1 |
| 2 |
∵∠BGE=90°,
∴∠BGC=90°,
∴△BGC的面积为:
| 1 |
| 2 |
∴△EBC的面积为:48.
故答案为:48.
点评:此题主要考查了重心的性质以及勾股定理的应用,根据已知得出△BGE是直角三角形是解题关键.

练习册系列答案
相关题目
下列图形中阴影部分的面积相等的是( )


| A、②③ | B、③④ | C、①② | D、①④ |

 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BC于点E.
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BC于点E. 某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为
某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为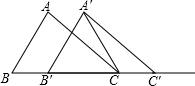 如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的周长为
如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移2个单位后,得到△A′B′C′,连接A′C,则△A′B′C的周长为 某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A等级的扇形的圆心角的大小为
某校根据去年初三学生参加中考的数学成绩的等级,绘制成如图的扇形统计图,则图中表示A等级的扇形的圆心角的大小为