题目内容
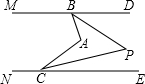 如图,已知,∠MBA+∠BAC+∠NCA=360°,
如图,已知,∠MBA+∠BAC+∠NCA=360°,(1)求证:MD∥NE.
(2)若∠ABD=70°,∠ACE=36°,BP和CP分别平分∠ABD,∠ACE,求∠BPC的度数.
考点:平行线的判定与性质
专题:计算题
分析:(1)过A作AF∥MD,根据平行线的性质得∠MBA+∠BAF=180°,而∠MBA+∠BAC+∠NCA=360°,则∠FAC+∠NCA=180°,于是根据平行线的判定得到AF∥NE,所以根据平行线于同一条直线的两直线平行得到MD∥NE;
(2)过P作PQ∥MD,先利用角平分线的定义得到∠DBP=
∠DBA=35°,∠ECP=
∠ACE=18°,再根据平行线的性质由PQ∥MD得∠DBP=∠BPQ=35°,由于MD∥NE,PQ∥MD,则PQ∥NE,所以∠QPC=∠PCE=18°,然后利用∠BPC=∠BPQ+∠QPC进行计算即可.
(2)过P作PQ∥MD,先利用角平分线的定义得到∠DBP=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: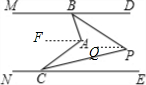 (1)过A作AF∥MD,如图,
(1)过A作AF∥MD,如图,
∴∠MBA+∠BAF=180°,
又∵∠MBA+∠BAC+∠NCA=360°,
∴∠FAC+∠NCA=180°,
∴AF∥NE,
∴MD∥NE;
(2)过P作PQ∥MD,
∵BP和CP分别平分∠ABD,∠ACE,
∴∠DBP=
∠DBA=
×70°=35°,∠ECP=
∠ACE=
×36°=18°,
∵PQ∥MD,
∴∠DBP=∠BPQ=35°,
∵MD∥NE,PQ∥MD,
∴PQ∥NE,
∴∠QPC=∠PCE=18°,
∴∠BPC=∠BPQ+∠QPC=53°.
 (1)过A作AF∥MD,如图,
(1)过A作AF∥MD,如图,∴∠MBA+∠BAF=180°,
又∵∠MBA+∠BAC+∠NCA=360°,
∴∠FAC+∠NCA=180°,
∴AF∥NE,
∴MD∥NE;
(2)过P作PQ∥MD,
∵BP和CP分别平分∠ABD,∠ACE,
∴∠DBP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵PQ∥MD,
∴∠DBP=∠BPQ=35°,
∵MD∥NE,PQ∥MD,
∴PQ∥NE,
∴∠QPC=∠PCE=18°,
∴∠BPC=∠BPQ+∠QPC=53°.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;同旁内角互补,两直线平行;平行线于同一条直线的两直线平行;两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
 已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.
已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交CD、AB于E、F,求证:AE=CF.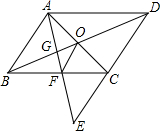 点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.
点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.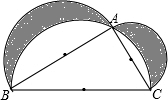 如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
如图,分别以直角三角形两直角边AB、AC及斜边BC为直径向外作半圆(以BC为直径的半圆过点A),∠BAC=90°,AB=4cm,AC=3cm,BC=5cm.求图中阴影部分的面积.
 如图,∠AOB=60°,点P在∠AOB的平分线上,∠CPD=120°,PD=2,求CD的长.
如图,∠AOB=60°,点P在∠AOB的平分线上,∠CPD=120°,PD=2,求CD的长. 如图,AB∥CD,∠1=(3x+50)°,∠2=(2x+30)°,则∠3的度数为
如图,AB∥CD,∠1=(3x+50)°,∠2=(2x+30)°,则∠3的度数为 C岛在B岛的北偏西48°方向,∠ACB等于95°,则C岛在A岛的
C岛在B岛的北偏西48°方向,∠ACB等于95°,则C岛在A岛的