题目内容
 如图,∠AOB=60°,点P在∠AOB的平分线上,∠CPD=120°,PD=2,求CD的长.
如图,∠AOB=60°,点P在∠AOB的平分线上,∠CPD=120°,PD=2,求CD的长.考点:全等三角形的判定与性质,角平分线的性质,勾股定理
专题:
分析:过点P作PE⊥OA于E,作PF⊥OB于F,作PG⊥CD于G,根据角平分线上的点到角的两边距离相等可得PE=PF,然后求出∠CPE=∠DPF,再利用“角边角”证明△PFD和△PEC全等,根据全等三角形对应边相等可得PC=PD,再根据等腰三角形的两底角相等求出∠PCD,根据直角三角形30°角所对的直角边等于斜边的一半可得PG=
PD,利用勾股定理列式求出DG,再根据等腰三角形三线合一的可得CD=2DG计算即可得解.
| 1 |
| 2 |
解答: 解:如图,过点P作PE⊥OA于E,作PF⊥OB于F,作PG⊥CD于G,
解:如图,过点P作PE⊥OA于E,作PF⊥OB于F,作PG⊥CD于G,
∵点P在∠AOB的平分线上,
∴PE=PF,
∵∠AOB=60°,
∴∠EPF=360°-90°×2-60°=120°,
∴∠DPF=120°-∠DPE,
∵∠CPD=120°,
∴∠CPE=120°-∠DPE,
∴∠CPE=∠DPF,
在△PFD和△PEC中,
,
∴△PFD≌△PEC(ASA),
∴PC=PD,
∵∠CPD=120°,
∴∠CDP=
(180°-120°)=30°,
∴PG=
PD=
×2=1,
在Rt△PDG中,由勾股定理得,DG=
=
=
,
∴CD=2DG=2
.
 解:如图,过点P作PE⊥OA于E,作PF⊥OB于F,作PG⊥CD于G,
解:如图,过点P作PE⊥OA于E,作PF⊥OB于F,作PG⊥CD于G,∵点P在∠AOB的平分线上,
∴PE=PF,
∵∠AOB=60°,
∴∠EPF=360°-90°×2-60°=120°,
∴∠DPF=120°-∠DPE,
∵∠CPD=120°,
∴∠CPE=120°-∠DPE,
∴∠CPE=∠DPF,
在△PFD和△PEC中,
|
∴△PFD≌△PEC(ASA),
∴PC=PD,
∵∠CPD=120°,
∴∠CDP=
| 1 |
| 2 |
∴PG=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△PDG中,由勾股定理得,DG=
| PD2-PG2 |
| 22-12 |
| 3 |
∴CD=2DG=2
| 3 |
点评:本题考查了全等三角形的判定与性质,等腰三角形的性质,角平分线上的点到角的两边距离相等的性质,勾股定理,熟记性质并作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A,B,直线CD与x轴、y轴分别交于点C,D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=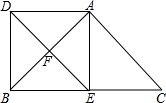 如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.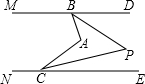 如图,已知,∠MBA+∠BAC+∠NCA=360°,
如图,已知,∠MBA+∠BAC+∠NCA=360°,
 如图,平行四边形ABCD的对角线AC、BD交于一点O,AB=11,△OCD的周长为27,则AC+BD=
如图,平行四边形ABCD的对角线AC、BD交于一点O,AB=11,△OCD的周长为27,则AC+BD=