题目内容
C岛在B岛的北偏西48°方向，∠ACB等于95°，则C岛在A岛的考点：方向角
专题：
分析：作CF∥AD，则AD∥CF∥BE，根据平行线的性质可得∠ACF=∠DAC，∠BCF=∠CBE，据此即可求得∠DAC的度数，从而求解．
解答：
解：作CF∥AD，则AD∥CF∥BE．
∵AD∥CF，
∴∠ACF=∠DAC，
同理∠BCF=∠CBE=48°，
∴∠DAC=∠ACB-∠BCF=95°-48°=47°，
则北偏东47°方向．
故答案是：北偏东47°．
解：作CF∥AD，则AD∥CF∥BE．∵AD∥CF，
∴∠ACF=∠DAC，
同理∠BCF=∠CBE=48°，
∴∠DAC=∠ACB-∠BCF=95°-48°=47°，
则北偏东47°方向．
故答案是：北偏东47°．
点评：本题考查了平行线的性质以及方向角的定义，正确作出辅助线是关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
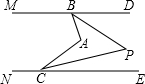如图，已知，∠MBA+∠BAC+∠NCA=360°，
如图，平行四边形ABCD的对角线AC、BD交于一点O，AB=11，△OCD的周长为27，则AC+BD=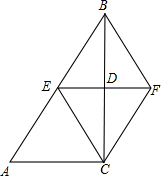
如图，在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，添加一个条件，能证明四边形BECF为正方形的是以下由线段a、b、c组成的三角形中，不是直角三角形的是（ ）
A、a=1，b=2，c=
| ||||
B、a=30，b=20，c=10
| ||||
| C、a=40，b=9，c=41 | ||||
D、a=3，b=
|