题目内容
18.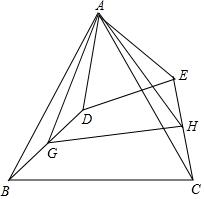 如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.
如图,△ABC中,AB=AC,∠BAC=α°(α为已知常数),以A为顶点作△ADE,使∠BAC=∠DAE,AD=AE,G、H分别为BD、CE的中点.(1)求证:AG=AH,且∠GAH=α°;
(2)延长BD与直线CE交于点P,补全图形,并求∠BPC的大小(用含α的代数式表示);
(3)设AB=a,直接写出点P到AB的最大距离.
分析 (1)先证明△ABD≌△ACE,得∠ADB=∠AEC,BD=CE,再证明△ADG≌△AEH,可得结论;
(2)根据△ABD≌△ACE,得∠ABD=∠ACE,所以∠P=∠BAC=α°;
(3)如图2中,作△ABC的外接圆,由(2)可知∠P=α=定值,推出点P在$\widehat{AC}$上运动,当点P′是优弧$\widehat{AB}$的中点P′时,点P′到AB的距离最大,作P′E⊥AB于E.求出P′E即可解决问题.
解答  证明:(1)∵∠BAC=∠DAE,
证明:(1)∵∠BAC=∠DAE,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAD=∠EAC,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴∠ADB=∠AEC,BD=CE,
∵G、H分别为BD、CE的中点,
∴DG=EH,
∴△ADG≌△AEH,
∴AG=AH,∠GAD=∠HAE,
∴∠GAD+∠DAH=∠HAE+∠DAH=α°,
即∠GAH=α°;
(2)如图1,由(1)得:△ABD≌△ACE,
∴∠ABD=∠ACE,
∴∠ABD+∠DBC+∠ACB=∠DBC+∠ACB+∠ACE,
∴∠P=∠BAC=α°.
(3)如图2中,作△ABC的外接圆,由(2)可知∠P=α=定值,
∴点P在$\widehat{AC}$上运动,当点P′是优弧$\widehat{AB}$的中点P′时,点P′到AB的距离最大,作P′E⊥AB于E.
∵$\widehat{AP′}$=$\widehat{BP′}$,P′E⊥AB,
∴P′A=P′B,AE=BE=$\frac{1}{2}$a,∠AP′E=′E=$\frac{1}{2}$∠AP′B=$\frac{1}{2}$∠ACB=$\frac{1}{2}$•$\frac{1}{2}$(180°-α)=45°-$\frac{1}{4}$α,
在Rt△AEP′中,tan∠AP′E=$\frac{AE}{P′E}$,
∴P′E=$\frac{\frac{1}{2}a}{tan(45°-\frac{1}{4}α)}$=$\frac{a}{2tan(45°-\frac{1}{4}α)}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、圆的有关知识,锐角三角函数,解直角三角形等知识,解题的关键是正确寻找全等三角形解决问题,重合添加辅助圆解决问题,属于中考压轴题.



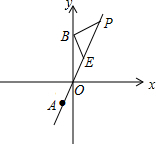 如图,点A(-1,-2)为正比例函数y=kx的图象上一点,B(0,4).
如图,点A(-1,-2)为正比例函数y=kx的图象上一点,B(0,4). 如图,为了求出湖两岸的A、B点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形,通过测量,得到AC长160米,BC长128米,问从点A穿过湖到点B有多远?
如图,为了求出湖两岸的A、B点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形,通过测量,得到AC长160米,BC长128米,问从点A穿过湖到点B有多远? 如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证:
如图,已知在△ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于点F,G是BF的中点.求证: