题目内容
18. 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠BOE的大小为75°.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠BOE的大小为75°.
分析 由矩形的性质得出∠BAD=∠ABC=90°,OA=OB,证明△AOB是等边三角形,得出AB=OB,∠ABO=60°,证出△ABE是等腰直角三角形,得出AB=BE,因此BE=OB,由等腰三角形的性质即可得出∠BOE的大小.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OB,∠ABO=60°,
∴∠OBE=30°,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∴BE=OB,
∴∠BOE=$\frac{1}{2}$(180°-30°)=75°;
故答案为:75°.
点评 本题考查了矩形的性质、等边三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的性质;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
6.若方程组$\left\{\begin{array}{l}{2kx+(k-1)y=3}\\{3x+4y=1}\end{array}\right.$的解x和y互为相反数,则k的值为( )
| A. | -4 | B. | 4 | C. | 2 | D. | -2 |
13.大学生小东到某快递公司做社会调查,了解到该快递公司为激励业务员的工作积极性,实行“月工资=基本工资+计件奖金”的办法,(计件奖金=月取送件数×每件奖金),并获得如下信息:
(1)求业务员的月基本工资和取送每件的奖金;
(2)若营业员丙月工资不低于2470元,这位营业员当月至少要取送多少件?
| 业务员 | 甲 | 乙 |
| 月取送件数/件 | 1200 | 900 |
| 月总收入/元 | 1920 | 1590 |
(2)若营业员丙月工资不低于2470元,这位营业员当月至少要取送多少件?
3.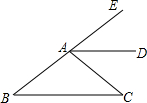 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠EAC的度数为( )| A. | 30° | B. | 40° | C. | 60° | D. | 80° |
8.已知3是关于x的方程$\frac{2}{3}$x2-2a+1=0的一个解,则2a的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
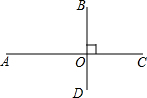 如图,已知线段AC、BD相互垂直,垂足为O,且OA>OC,OB>OD.
如图,已知线段AC、BD相互垂直,垂足为O,且OA>OC,OB>OD.