题目内容
7.某校对八年级一班学生所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号)
根据以上信息,解答下列问题
(1)在条形统计图中,请把空缺部分补充完整.
(2)写出这组数据中的众数和中位数.
(3)在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小.
分析 (1)先求出总人数,再求出现175的人数,从而得到出现185的人数,即可补充图形;
(2)由统计图可得众数是165和170,中位数是170;
(3)利用185型校服所对应的扇形圆心角=185型校服有百分比×360°求解即可.
解答 解:(1)总人数为:15÷30%=50(人),
175的人数为:50×20%=10(人),
185的人数为:50-3-15-15-10-5=2(人),
补充统计图为:
(2)由统计图可得众数是165和170,中位数是170;
(3)185型校服所对应的扇形圆心角为:$\frac{2}{50}$×360°=14.4°.
点评 本题主要考查了条形统计图,扇形统计图,中位数及众数,解题的关键是读懂统计图,获得准确的信息.

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | 2$\sqrt{5}$×3$\sqrt{5}$=6×25=150 | B. | 2$\sqrt{5}$×3$\sqrt{5}$=6×5=30 | C. | 2$\sqrt{5}$×3$\sqrt{5}$=6$\sqrt{5}$ | D. | 2$\sqrt{5}$×3$\sqrt{5}$=5$\sqrt{5}$ |
15.一名学生军训时连续射靶10次,命中环数分别为 7,8,6,8,5,9,10,7,6,4.则这名学生射击环数的方差是( )
| A. | 3 | B. | 2.9 | C. | 2.8 | D. | 2.7 |
12.若不等式组$\left\{\begin{array}{l}{x<2m+1}\\{x>7-m}\end{array}\right.$无解,则m的取值范围是( )
| A. | m=2 | B. | m<2 | C. | m≤2 | D. | m≥2 |
16.已知x=2是不等式-3(mx-3m+2)≤0的解,且x=1不是这个不等式的解,则实数m的取值范围是( )
| A. | m>1 | B. | m<2 | C. | 1<m≤2 | D. | 1≤m≤2 |
 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠BOE的大小为75°.
如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠BOE的大小为75°.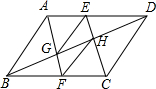 如图,平行四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是对角线BD上的三等分点.
如图,平行四边形ABCD中,点E、F分别是AD、BC的中点,G、H分别是对角线BD上的三等分点.