题目内容
6.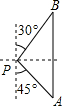 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )| A. | 60$\sqrt{3}$ n mile | B. | 60$\sqrt{2}$ n mile | C. | 30$\sqrt{3}$ n mile | D. | 30$\sqrt{2}$ n mile |
分析 如图作PE⊥AB于E.在Rt△PAE中,求出PE,在Rt△PBE中,根据PB=2PE即可解决问题.
解答 解:如图作PE⊥AB于E.
在Rt△PAE中,∵∠PAE=45°,PA=60n mile,
∴PE=AE=$\frac{\sqrt{2}}{2}$×60=30$\sqrt{2}$n mile,
在Rt△PBE中,∵∠B=30°,
∴PB=2PE=60$\sqrt{2}$n mile,
故选B
点评 本题考查方向角、直角三角形、锐角三角函数的有关知识.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
14.使函数y=$\sqrt{3-x}$有意义的自变量x的取值范围是( )
| A. | x≥3 | B. | x≥0 | C. | x≤3 | D. | x≤0 |
18.下列实数中,无理数是( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -2 | D. | $\frac{2}{7}$ |
15.2016年,我国国内生产总值达到74.4万亿元,数据“74.4万亿”用科学记数法表示( )
| A. | 74.4×1012 | B. | 7.44×1013 | C. | 74.4×1013 | D. | 7.44×1015 |
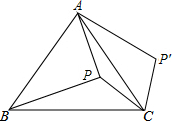 如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为$\frac{3}{5}$.
如图,点P在等边△ABC的内部,且PC=6,PA=8,PB=10,将线段PC绕点C顺时针旋转60°得到P'C,连接AP',则sin∠PAP'的值为$\frac{3}{5}$.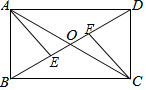 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.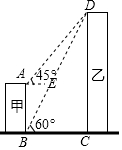 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)