题目内容
9.在平面直角坐标系中,一次函数y=x的图象、反比例函数y=$\frac{1.1}{x}$图象以及二次函数y=x2-6x的对称轴围成一个封闭的平面区域(含边界),从该区域内所有格点(横、纵坐标均为整数的点称为格点)中任取3个,则该3点恰能作为一个三角形的三个顶点的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
分析 先画出正比例函数、反比例函数和抛物线的图象,再确定抛物线的对称轴,接着通过计算确定封闭的平面区域(含边界)所有满足条件的格点坐标,然后利用列举法展示所有可能的结果数,再找出能构成三角形的结果数,于是可根据概率公式计算出3点恰能作为一个三角形的三个顶点的概率.
解答 解:如图,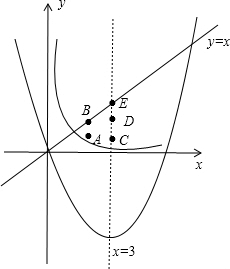 二次函数y=x2-6x的对称轴为直线x=$\frac{6}{2}$=3,
二次函数y=x2-6x的对称轴为直线x=$\frac{6}{2}$=3,
当x=$\frac{1.1}{x}$,解得x=±$\sqrt{1.1}$,
因为$\sqrt{1.1}$>1,
所以封闭的平面区域(含边界)不含横坐标为1的点,
当x=2时,y=x=2,而y=$\frac{1.1}{x}$=0.55,则点A(2,1)、点B(2,2)满足条件的点;
当x=3时,y=x=3,而y=$\frac{1.1}{x}$≈0.37,则点C(3,1)、点D(3,2)、点E(3,3)为满足条件的点;
从5个点中任取3个点共有(ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE)10中等可能的结果数,其中
有9种结果数作为一个三角形,所以3点恰能作为一个三角形的三个顶点的概率是$\frac{9}{10}$.
故选D.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.也考查了正比例函数、反比例函数和二次函数图象的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某学校组织学生进行社会主义核心价值观的知识竞赛,进入决赛的共有20名学生,他们的决赛成绩如下表所示:
那么20名学生决赛成绩的众数和中位数分别是( )
| 决赛成绩/分 | 95 | 90 | 85 | 80 |
| 人数 | 4 | 6 | 8 | 2 |
| A. | 85,90 | B. | 85,87.5 | C. | 90,85 | D. | 95,90 |
17. 如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
 如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )| A. | 10 | B. | 12 | C. | 18 | D. | 24 |
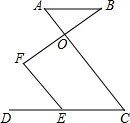 如图,AB∥DC,O是AC上一点,E是CD上一点,F是射线BO上一点,且∠DEF=∠A.
如图,AB∥DC,O是AC上一点,E是CD上一点,F是射线BO上一点,且∠DEF=∠A.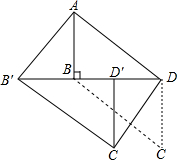 如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.
如图,在?ABCD中,AB⊥BD,AB=6,AD=3$\sqrt{13}$,将△BCD沿DB方向移动t个单位,得到△B′C′D′,连接AB′,C′D.