题目内容
14.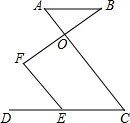 如图,AB∥DC,O是AC上一点,E是CD上一点,F是射线BO上一点,且∠DEF=∠A.
如图,AB∥DC,O是AC上一点,E是CD上一点,F是射线BO上一点,且∠DEF=∠A.(1)求证:FE∥OC;
(2)若∠B=30°,∠DEF=60°,求证:EF⊥BF.
分析 (1)根据平行线的性质得出∠A=∠C,求出∠DEF=∠C,根据平行线的判定推出即可;
(2)求出∠A,根据三角形的外角求出∠AOF,根据平行线的性质得出∠F=∠AOF=90°,根据定义得出即可.
解答 (1)证明:∵AB∥DC,
∴∠A=∠C,
∵∠DEF=∠A,
∴∠DEF=∠C,
∴FE∥DC;
(2)证明:∵由(1)知:∠A=∠C=∠DEF,
又∵∠DEF=60°,
∴∠A=60°,
∵∠B=30°,
∴∠AOF=∠A+∠B=90°,
∵AC∥EF,
∴∠F=∠AOF=90°,
∴EF⊥BF.
点评 本题考查了平行线的性质和判定,垂直定义,三角形的外角性质的应用,能灵活运用平行线的判定和性质进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
4.在实数0,$\sqrt{3}$,-$\frac{2}{3}$,|-2|中,最小的是( )
| A. | $\sqrt{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | |-2| |
2.在-3.14,$\sqrt{2}$,0,π,0.1010010001…,$\sqrt{16}$中,无理数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.在平面直角坐标系中,一次函数y=x的图象、反比例函数y=$\frac{1.1}{x}$图象以及二次函数y=x2-6x的对称轴围成一个封闭的平面区域(含边界),从该区域内所有格点(横、纵坐标均为整数的点称为格点)中任取3个,则该3点恰能作为一个三角形的三个顶点的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
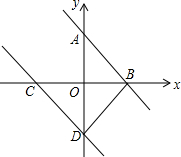 如图,已知一条直线经过点A(0,3)、点B(2,0),将这条直线向左平移与x轴、y轴分别交于点C、点D.若DB=DC,求直线CD的函数解析式.
如图,已知一条直线经过点A(0,3)、点B(2,0),将这条直线向左平移与x轴、y轴分别交于点C、点D.若DB=DC,求直线CD的函数解析式.



