题目内容
4.已知圆O的直径AB=4,半径OC⊥AB,在射线OB上有一点D,且点D与圆O上各点所连接线段最短为1,则CD=$\sqrt{5}$或$\sqrt{13}$.分析 利用点D在OB上,得到BD=1,然后分类讨论:当点在⊙O外,OD=OB+BD=3,在Rt△COD中,利用勾股定理可计算出CD=$\sqrt{13}$;当点在⊙O内,OD′=OB-BD′=1,利用勾股定理可计算出CD′=$\sqrt{5}$,于是得到CD的长为$\sqrt{5}$或$\sqrt{13}$.
解答 解:如图,∵直径AB=4,
∴OB=2,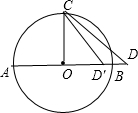 ∵OC⊥AB,
∵OC⊥AB,
∴∠COB=90°,
∵点D与圆O上各点所连接线段最短为1,
∴BD=1,
当点在⊙O外,OD=OB+BD=2+1=3,
在Rt△COD中,CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=$\sqrt{13}$;
当点在⊙O内,OD′=OB-BD′=2-1=1,
在Rt△COD中,CD′=$\sqrt{O{C}^{2}+OD{′}^{2}}$=$\sqrt{5}$,
∴CD的长为$\sqrt{5}$或$\sqrt{13}$.
故答案为$\sqrt{5}$或$\sqrt{13}$.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了勾股定理.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9.在平面直角坐标系中,一次函数y=x的图象、反比例函数y=$\frac{1.1}{x}$图象以及二次函数y=x2-6x的对称轴围成一个封闭的平面区域(含边界),从该区域内所有格点(横、纵坐标均为整数的点称为格点)中任取3个,则该3点恰能作为一个三角形的三个顶点的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{10}$ | D. | $\frac{9}{10}$ |
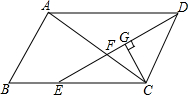 如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.
如图,?ABCD中,AB=3cm,AD=6cm,∠ADC的平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=$\frac{3}{2}$$\sqrt{3}$cm,则EF的长为$\sqrt{3}$cm.