题目内容
14.若点P(-1-2a,2a-4)关于原点对称的点在第一象限内,则a的整数解有2个.分析 根据点P(-1-2a,2a-4)关于原点对称的点在第一象限内,可得点P在第三象限,然后根据第三象限内点的坐标特点可得a的取值范围,然后可得a的整数解.
解答 解:∵点P(-1-2a,2a-4)关于原点对称的点在第一象限内,
∴点P在第三象限,
∴$\left\{\begin{array}{l}{-1-2a<0}\\{2a-4>0}\end{array}\right.$,
解得:-$\frac{1}{2}$<a<2,
∵a为整数,
∴a=0或1,共2个,
故答案为:2.
点评 此题主要考查了关于原点对称的点的坐标特征,以及四个象限内点的坐标符号,关键是掌握两个点关于原点对称时,它们的坐标符号相反.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.数据-1,0,1,2,3的极差是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
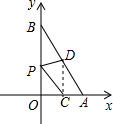 如图,一次函数y=kx+b的图象与x、y轴分别交于点A(2,0)、B(0,4).O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,则当P点坐标为(0,1)时,PC+PD的最小值为2$\sqrt{2}$.
如图,一次函数y=kx+b的图象与x、y轴分别交于点A(2,0)、B(0,4).O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,则当P点坐标为(0,1)时,PC+PD的最小值为2$\sqrt{2}$.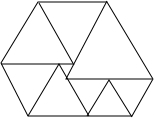 如图,是由9个等边三角形拼成的一个六边形,如果中间最小的等边三角形的边长是1,则此右上角的最大的正三角形的边长是6.
如图,是由9个等边三角形拼成的一个六边形,如果中间最小的等边三角形的边长是1,则此右上角的最大的正三角形的边长是6. 如图,在△ABC中,点I是内心,且∠BIC=124°,则∠A=68°.
如图,在△ABC中,点I是内心,且∠BIC=124°,则∠A=68°.