题目内容
4.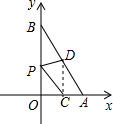 如图,一次函数y=kx+b的图象与x、y轴分别交于点A(2,0)、B(0,4).O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,则当P点坐标为(0,1)时,PC+PD的最小值为2$\sqrt{2}$.
如图,一次函数y=kx+b的图象与x、y轴分别交于点A(2,0)、B(0,4).O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,则当P点坐标为(0,1)时,PC+PD的最小值为2$\sqrt{2}$.
分析 先由中点坐标公式求得点D、C的坐标,然后作点C关于y轴的对称点C′,连接C′D交y轴与点P,由题意可知点O是CC′的中点,故此OP=$\frac{1}{2}DC$=1,从而可求得点P的坐标,由两点之间的距离公式可求得C′D的长度即可.
解答 解:如图所示;作点C关于y轴的对称点C′,连接C′D交y轴与点P.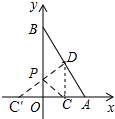
∵A(2,0)、B(0,4),点C、D分别为OA、AB的中点,
∴D(1,2)、C(1,0).
∵点C′与点C关于y轴对称,
∴点C′(-1,0),PC=PC′.
∴O为CC′的中点.
∴OP=$\frac{1}{2}DC$=1.
∴P(0,1).
∴PD+PC=PD+PC′=C′D.
由两点间的距离公式可知;C′D=$\sqrt{(-1-1)^{2}+(2-0)^{2}}$=2$\sqrt{2}$.
故答案为:(0,1);2$\sqrt{2}$.
点评 本题主要考查的是轴对称路径最短问题,明确点C′,P,D在一条直线上时PC+PD有最小值是解题的关键.

练习册系列答案
相关题目
14.某班七个合作学习小组人数如下:4,5,5,x,6,7,8,已知这组数据的平均数为6,则这组数据的中位数和众数是( )
| A. | 5,5 | B. | 6,5 | C. | 6,5和6 | D. | 6,5和7 |
15.若分式$\frac{3}{x-5}$有意义,则x满足的条件是( )
| A. | x≠0 | B. | x≥5 | C. | x≠5 | D. | x≤5 |
16.用加减法解方程组$\left\{\begin{array}{l}{11x+3z=9}\\{3x+2y+z=8}\\{2x-6y+4z=5}\end{array}\right.$,较方便的是( )
| A. | 先消去x,再解$\left\{\begin{array}{l}{22y+2z=61}\\{66y-38z=-33}\end{array}\right.$ | |
| B. | 先消去y,再解$\left\{\begin{array}{l}{11x+7z=29}\\{11x+3z=9}\end{array}\right.$ | |
| C. | 先消去z,再解$\left\{\begin{array}{l}{11x+3z=9}\\{11x+14y=27}\end{array}\right.$ | |
| D. | 先消去z,再解$\left\{\begin{array}{l}{2x-6y=-15}\\{19x+9y=8}\end{array}\right.$ |