题目内容
2．
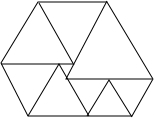如图，是由9个等边三角形拼成的一个六边形，如果中间最小的等边三角形的边长是1，则此右上角的最大的正三角形的边长是6．
分析 设第二小的等边三角形的边长为x，而中间的小等边三角形的边长是1，根据等边三角形的三边都相等可得到其它等边三角形的边长分别x+1，x+2，x+3，利用最大三角形的边长相等得出方程x+3=2x，求得x，进一步得出答案即可．
解答 解：如图，
设第二小的等边三角形的边长为x，而中间的小等边三角形的边长是1，
所以其它等边三角形的边长分别x+1，x+2，x+3，
由图形得，x+3=2x，
解得x=3，
则x+3=6，
答：此右上角的最大的正三角形的边长是6．
故答案为：6．
点评 此题考查一元一次方程的实际运用，等边三角形的性质，根据图形，设出未知数，利用大等边三角形的边长建立方程解决问题．
练习册系列答案
相关题目
13．在平面直角坐标系中，已知点P0的坐标为（1，0）．将点P0绕着原点O按顺时针方向旋转45°得点P1，延长OP1到点P2，使OP2=2OP1；再将点P2绕着原点O按顺时针方向旋转45°得点P3，延长OP3到点P4，使OP4=2OP3，…，如此进行下去，则线段OP2014的长为（ ）
| A． | 22014 | B． | 22013 | C． | 21007 | D． | 21006 |
10．在平面直角坐标系xOy中，已知点A（0，1），B（1，2），点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是（ ）
| A． | （-1，0） | B． | （-2，0） | C． | （0，0） | D． | （1，0） |
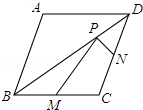已知菱形ABCD的两条对角线分别为5和12，M、N分别是边BC、CD的中点，P是对角线BD上一点，则PM+PN的最小值=6.5．