题目内容
 如图,四边形ABCD中,∠B=∠C=90°,AM、DM分别是∠DAB与∠ADC的角平分线,AD=10,BC=6,则△ADM的面积为
如图,四边形ABCD中,∠B=∠C=90°,AM、DM分别是∠DAB与∠ADC的角平分线,AD=10,BC=6,则△ADM的面积为考点:角平分线的性质
专题:
分析:过M作ME⊥AD,由角平分线的性质可得ME=MC=MB=3,再利用直角三角形的面积进行计算即可.
解答:解:
过M作ME⊥AD,
∵DM平分∠ADC,MC⊥DC,ME⊥DA,
∴MC=ME,
同理可得ME=MB,
∴ME=
BC=3,
∴S△ADM=
AD•ME=
×10×3=15,
故答案为:15.
过M作ME⊥AD,
∵DM平分∠ADC,MC⊥DC,ME⊥DA,
∴MC=ME,
同理可得ME=MB,
∴ME=
| 1 |
| 2 |
∴S△ADM=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:15.
点评:本题主要考查角平分线的性质,根据角平分线上的点到角两边的距离相等求得ME是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示,其中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
已知一个三角形的三边长分别为a、b、c,且它们满足(a+b)2-c2=2ab,则该三角形的形状为( )
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
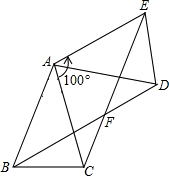 如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F. 如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图.
如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图.
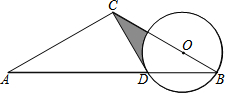 如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D.已知经过点D的⊙O切线恰好经过点C.