题目内容
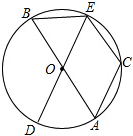如图，AB、DE是⊙O的直径，C是⊙O上的一点，且 |
| AD |
|
| CE |
考点：圆心角、弧、弦的关系,圆周角定理
专题：计算题
分析：根据对顶角相等得到∠AOD=∠BOE，再根据圆心角、弧、弦的关系得
=
，加上
=
，所以
=
，于是有BE=CE．
 |
| AD |
|
| BE |
|
| AD |
|
| CE |
|
| BE |
|
| CE |
解答：解：BE=CE．理由如下：
∵AB、DE是⊙O的直径，
∴∠AOD=∠BOE，
∴
=
，
∵
=
，
∴
=
，
∴BE=CE．
∵AB、DE是⊙O的直径，
∴∠AOD=∠BOE，
∴
|
| AD |
|
| BE |
∵
|
| AD |
|
| CE |
∴
|
| BE |
|
| CE |
∴BE=CE．
点评：本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
相关题目
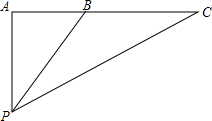为制作一部海洋专题片，一摄像师在一直升飞机上进行航拍，飞机在同一高度沿一条直线飞行，飞机每秒钟飞行20米．当飞机飞到A点时，摄像师发现自己的正下方的海面上有一美丽景色P，一段时间后飞机飞到B点，此时测得其俯角是35.1°，又经过了半分钟，飞机飞到C点，此时测得此俯角是16.8°，由此你能知道飞机的大约高度吗？（参考数据：sin35.1°=0.58，cos35.1°=0.82，tan35.1°=0.70，sin16.8°=0.29，cos16.8°=0.96，tan16.8°=0.30）
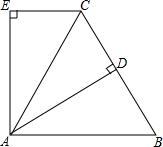已知：如图，△ABC是等边三角形，AD⊥BC于D，CE∥AB，且AE⊥EC，求证：AE=AD．