题目内容
已知
=1，求证：y=6x．
| a2-9x2+6xy-y2 |
| (a+3x)2-(ay+3xy) |
考点：分式的混合运算
专题：证明题
分析：把已知等式的分子分母因式分解，约分后得到
=1，然后去分母整理即可得到结论．
| a-3x+y |
| a+3x |
解答：证明：∵
=1，
∴
=1，
∴
=1，
∴
=1，
∴a-3x+y=a+3x，
∴y=6x．
| a2-9x2+6xy-y2 |
| (a+3x)2-(ay+3xy) |
∴
| a2-(3x-y)2 |
| (a+3x)2-y(a+3x) |
∴
| (a+3x-y)(a-3x+y) |
| (a+3x)(a+3x-y) |
∴
| a-3x+y |
| a+3x |
∴a-3x+y=a+3x，
∴y=6x．
点评：本题考查了分式方程的混合运算：分式的混合运算，要注意运算顺序，式与数有相同的混合运算顺序；先乘方，再乘除，然后加减，有括号的先算括号里面的．
练习册系列答案
相关题目
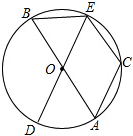如图，AB、DE是⊙O的直径，C是⊙O上的一点，且
潜望镜中，两面镜子互相平行放置，你知道为什么进入潜望镜的光线和离开潜望镜的光线平行吗？