题目内容
小王发现32-12=8，52-32=16，72-52=24，92-72=32…由此他归纳出：两个连续奇数的平方差能被8整除，你认为小王归纳的结论正确吗？为什么？
考点：因式分解的应用,规律型：数字的变化类
专题：常规题型
分析：观察前面的等式，根据平方差公式得到第n个等式为（2n+1）2-（2n-1）2=4n•2=8n，因此可判断两个连续奇数的平方差能被8整除．
解答：解：小王归纳的结论正确．理由如下：
32-12=（3+1）（3-1）=4×2=8×1，
52-32=（5+3）（5-3）=8×2，
72-52=（7+5）（7-5）=12×2=8×3=24，
92-72=（9+7）（9-7）=16×2=8×4=32，
…
第n个等式为（2n+1）2-（2n-1）2=（2n+1+2n-1）（2n+1-2n+1）=4n•2=8n，
所以两个连续奇数的平方差能被8整除．
32-12=（3+1）（3-1）=4×2=8×1，
52-32=（5+3）（5-3）=8×2，
72-52=（7+5）（7-5）=12×2=8×3=24，
92-72=（9+7）（9-7）=16×2=8×4=32，
…
第n个等式为（2n+1）2-（2n-1）2=（2n+1+2n-1）（2n+1-2n+1）=4n•2=8n，
所以两个连续奇数的平方差能被8整除．
点评：本题考查了因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．
练习册系列答案
相关题目
如图，⊙O是△ABC的外接圆，∠BAC=60°，点P在AO上（点P不与A、O重合），则∠BPC可能为
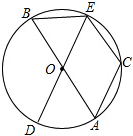如图，AB、DE是⊙O的直径，C是⊙O上的一点，且
潜望镜中，两面镜子互相平行放置，你知道为什么进入潜望镜的光线和离开潜望镜的光线平行吗？