题目内容
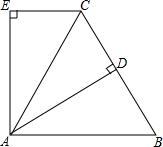已知：如图，△ABC是等边三角形，AD⊥BC于D，CE∥AB，且AE⊥EC，求证：AE=AD．考点：角平分线的性质,等边三角形的性质
专题：证明题
分析：根据条件可得∠EAC=30°，可得到∠ECA=∠ACD，利用角平分线的性质可得到AE=AD．
解答：证明：
∵△ABC为等边三角形，
∴∠CAB=∠ACB=60°，
∵CE∥AB，
∴∠ECA=∠CAB=60°，
∴AC平分∠ECD，
∵AD⊥BC，AE⊥EC，
∴AE=AD．
∵△ABC为等边三角形，
∴∠CAB=∠ACB=60°，
∵CE∥AB，
∴∠ECA=∠CAB=60°，
∴AC平分∠ECD，
∵AD⊥BC，AE⊥EC，
∴AE=AD．
点评：本题主要考查等边三角形的性质和角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
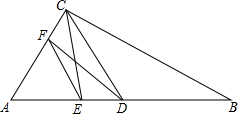如图，在△ABC中，中线CD⊥AC，CD=AC，点E在AB上，且AE=
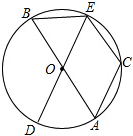如图，AB、DE是⊙O的直径，C是⊙O上的一点，且