题目内容
已知x,y,z满足|x-z-2|+|3x-3y-3|=-(3y+2z-13)2,求xyz的值.
考点:解三元一次方程组,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:利用非负数的性质,将所给的绝对值方程转化为三元一次方程组,解方程组即可解决问题.
解答:解:∵|x-z-2|+|3x-3y-3|=-(3y+2z-13)2,
∴|x-z-2|+|3x-3y-3|+(3y+2z-13)2=0,
∵|x-z-2|≥0,|3x-3y-3|≥0,(3y+2z-13)2≥0,
∴
,
由②÷3得:x-y-1=0④,
由①-④得:y-z-1=0⑤,
由③+2×⑤得:5y=15,y=3;
将y=3代入④得:x=4;
将y=3代入⑤得:z=2,
∴xyz=24.
∴|x-z-2|+|3x-3y-3|+(3y+2z-13)2=0,
∵|x-z-2|≥0,|3x-3y-3|≥0,(3y+2z-13)2≥0,
∴
|
由②÷3得:x-y-1=0④,
由①-④得:y-z-1=0⑤,
由③+2×⑤得:5y=15,y=3;
将y=3代入④得:x=4;
将y=3代入⑤得:z=2,
∴xyz=24.
点评:该题主要考查了非负数的应用、三元一次方程组的解法及其应用问题等重要代数知识点;对求解运算能力、整体代换思想等均提出了较高的要求.

练习册系列答案
相关题目
 已知,如图,△ABC内接于圆O,D是
已知,如图,△ABC内接于圆O,D是
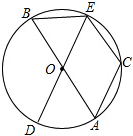 如图,AB、DE是⊙O的直径,C是⊙O上的一点,且
如图,AB、DE是⊙O的直径,C是⊙O上的一点,且 潜望镜中,两面镜子互相平行放置,你知道为什么进入潜望镜的光线和离开潜望镜的光线平行吗?
潜望镜中,两面镜子互相平行放置,你知道为什么进入潜望镜的光线和离开潜望镜的光线平行吗?