��Ŀ����
7��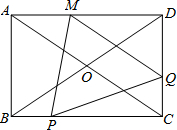 ��ͼ������ABCD�У��Խ���AC��BD���ڵ�O��AB=6��BC=8������P�ӵ�B������BC������ÿ��1����λ���ȵ��ٶ����C�����˶���ͬʱ����Q�ӵ�C������CD������ÿ��1����λ���ȵ��ٶ����D�����˶���������һ���㵽���յ��ֹͣ�˶�������Q��QM��AC��AD�ڵ�M������PM��PQ�����P���˶�ʱ��Ϊt�룬��PQM�����Ϊs��
��ͼ������ABCD�У��Խ���AC��BD���ڵ�O��AB=6��BC=8������P�ӵ�B������BC������ÿ��1����λ���ȵ��ٶ����C�����˶���ͬʱ����Q�ӵ�C������CD������ÿ��1����λ���ȵ��ٶ����D�����˶���������һ���㵽���յ��ֹͣ�˶�������Q��QM��AC��AD�ڵ�M������PM��PQ�����P���˶�ʱ��Ϊt�룬��PQM�����Ϊs����1����tΪ��ֵʱ��PQ��BD��
��2����S��t֮��ĺ�����ϵʽ����ȷ���Ա���t��ȡֵ��Χ��
��3�����˶��������Ƿ����ijһʱ��t��ʹ��PQM����������ABCD����ıȵ���9��32�������ڣ����t��ֵ���������ڣ�˵�����ɣ�
���� ��1�����ݾ��ε����ʡ����������ε��ж������ʵõ�����ʽ�����㼴�ɣ�
��2���������������ε��������AM�����ݾ��ε������ʽ�����ε������ʽ�Լ������ε������ʽ���㼴�ɣ�
��3�����������г�һԪ���η��̣��ⷽ�̼��ɣ�
��� �⣺��1�����ı���ABCD�Ǿ��Σ�
��AD=BC=8��CD=AB=6
��PQ��BD��
���DBC=��QPC����CDB=��CQP��
���CBD�ס�CPQ
��$\frac{CP}{CB}$=$\frac{CQ}{CD}$����$\frac{8-t}{8}$=$\frac{t}{6}$��
��ã�t=$\frac{24}{7}$��
�൱t=$\frac{24}{7}$ʱ��PQ��BD��
��2����MQ��AC��
���ACD�ס�MQD��
��$\frac{AD}{DM}$=$\frac{DC}{CQ}$����$\frac{8}{8-AM}$=$\frac{6}{6-t}$��
��ã�AM=$\frac{4}{3}$t��
�����⣬S=����ABCD�����-����ABPM�����-��DMQ�����-��PCQ�����
=6��8-$\frac{1}{2}��$��t+$\frac{4}{3}$t����6-$\frac{1}{2}��$��8-t����t-$\frac{1}{2}��$��8-$\frac{4}{3}$t����6-t��
=-$\frac{1}{6}$t2-3t+24��
�Ա���t��ȡֵ��Χ��0��t��6��
��3��������ã�-$\frac{1}{6}$t2-3t+24=$\frac{9}{32}$��48��
�����ã�t2+18t-63=0��
��ã�t1=3��t2=-21���������⣬��ȥ����
�൱t=3��ʱ����PQM����������ABCD����ıȵ���9��32��
���� ���⿼����Ǿ��ε����ʡ����������ε��ж������ʣ����κ�������ʽ��ȷ��������������������ε��ж����������ʶ�����������ε��ĸ��Ƕ���ֱ���ǽ���Ĺؼ���

 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�| A�� | $\sqrt{12}$-$\sqrt{2}$ | B�� | $\sqrt{18}$-$\sqrt{8}$ | C�� | $\sqrt{8{a}^{2}}$+$\sqrt{2a}$ | D�� | $\sqrt{{x}^{2}y}$+$\sqrt{x{y}^{2}}$ |
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
| A�� | -3 | B�� | 3 | C�� | $\frac{1}{3}$ | D�� | ��3 |
 ��ͼ����ij�ֹ������丩��ͼ����˹���������ͼ�ǣ�������
��ͼ����ij�ֹ������丩��ͼ����˹���������ͼ�ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | 9 | B�� | -9 | C�� | ��9 | D�� | 81 |
 ��ͼ����֪�ڳ�����ABCD�У�AD=10��CD=5����E�ӵ�D���������߶�DA��ÿ��1����λ�����ٶ����A�����ƶ���ͬʱ��F�ӵ�C������������CD������ÿ��2����λ�����ٶ��ƶ�����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ʱBF��CE�����E�ƶ���ʱ��Ϊt���룩��
��ͼ����֪�ڳ�����ABCD�У�AD=10��CD=5����E�ӵ�D���������߶�DA��ÿ��1����λ�����ٶ����A�����ƶ���ͬʱ��F�ӵ�C������������CD������ÿ��2����λ�����ٶ��ƶ�����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ʱBF��CE�����E�ƶ���ʱ��Ϊt���룩��