题目内容
15.在以下实数$\frac{π}{3}$,$\frac{\sqrt{2}}{2}$,1.732,$\frac{22}{7}$中,无理数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 无理数就是无限不循环小数,根据定义即可判断.
解答 解:无理数有:$\frac{π}{2}$,$\frac{\sqrt{2}}{2}$共2个.
故选C.
点评 此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{6}$,0.8080080008…(每两个8之间依次多1个0)等形式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.一元一次不等式2x+1≥0的解集是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x≥-$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$ |
3.在实数$\sqrt{4}$、$\sqrt{3}$、$\frac{22}{7}$、0.$\stackrel{.}{3}$、π、$\root{3}{9}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.设a=$\sqrt{43}-1$,a在两个相邻整数之间,则这两个整数是( )
| A. | 2和3 | B. | 3和4 | C. | 4和5 | D. | 5和6 |
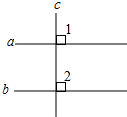 如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.
如图,已知a∥b,如果c⊥a,判断c与b的位置关系,并说明理由.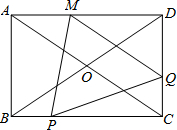 如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动.过点Q作QM∥AC交AD于点M,连接PM,PQ.设点P的运动时间为t秒,△PQM的面积为s.
如图,矩形ABCD中,对角线AC,BD交于点O,AB=6,BC=8.动点P从点B出发沿BC方向,以每秒1个单位长度的速度向点C匀速运动,同时动点Q从点C出发沿CD方向,以每秒1个单位长度的速度向点D匀速运动,当其中一个点到达终点后即都停止运动.过点Q作QM∥AC交AD于点M,连接PM,PQ.设点P的运动时间为t秒,△PQM的面积为s.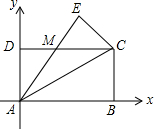 如图,在平面直角坐标系中,有一矩形ABCD,其中A(0,0),B(m,0),D(0,n),m是最接近$\sqrt{65}$的整数,n是16的算术平方根,若将△ABC沿矩形对角线AC所在直线翻折,点B落在点E处,AE与边CD相交于点M.
如图,在平面直角坐标系中,有一矩形ABCD,其中A(0,0),B(m,0),D(0,n),m是最接近$\sqrt{65}$的整数,n是16的算术平方根,若将△ABC沿矩形对角线AC所在直线翻折,点B落在点E处,AE与边CD相交于点M.