题目内容
7. 在平面直角坐标系xOy中,等腰三角形ABC的三个顶点A(0,1),点B在x轴的正半轴上,∠ABO=30°,点C在y轴上.
在平面直角坐标系xOy中,等腰三角形ABC的三个顶点A(0,1),点B在x轴的正半轴上,∠ABO=30°,点C在y轴上.(1)直接写出点C的坐标:(0,-1)或(0,3);
(2)点P关于直线AB的对称点P′在x轴上,AP=1,在图中标出点P的位置并说明理由.
分析 (1)设出点C坐标,三角形ABC为等腰三角形分三种情况,结合两点间的距离公式分情况讨论即可得出结论;
(2)由对称的特性结合到点的距离为固定值得图象为圆,可得出点P的位置.
解答 解:(1)根据题意完善图形,如图1所示.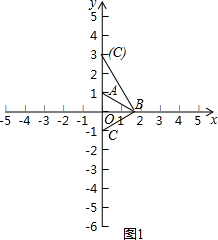
∵∠ABO=30°,点A(0,1),
∴OA=1,tan∠ABO=$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$,AB=$\frac{OA}{sin∠ABO}$=2,
∴点B的坐标为($\sqrt{3}$,0).
∵点C在y轴上,
∴设点C的坐标为(0,m).
∵三角形ABC为等腰三角形,
∴分三种情况考虑:
①当AC=AB时,由两点间的距离公式可知:
$\sqrt{{0}^{2}+(m-1)^{2}}$=2,解得:m=-1,或m=3,
即点C的坐标为(0,-1)或(0,3);
②当AC=BC时,由两点间的距离公式可知:
$\sqrt{{0}^{2}+(m-1)^{2}}$=$\sqrt{(0-\sqrt{3})^{2}+(m-0)^{2}}$,解得:m=-1,
即点C的坐标为(0,-1);
③当AB=BC时,由两点间的距离公式可知:
2=$\sqrt{(0-\sqrt{3})^{2}+(m-0)^{2}}$,解得m=-1或m=1(舍去),
即点C的坐标为(0,-1).
综上得:点C的坐标为:(0,-1)或(0,3).
故答案为:(0,-1)或(0,3).
(2)第一步:以A点为圆心,1为半径作圆,⊙A与x轴切与原点O,
第二步:过点O作OP⊥AB交⊙A于点P,P点即为所求(图形如图2).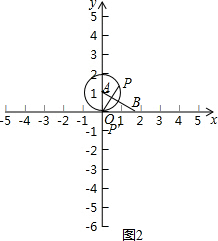
∵点P与点P′关于直线AB对称,且AP=1,
∴AP′=AP=1.
故用上面的画法寻找点P.
点评 本题考查了两点间的距离公式、等腰三角形的性质以及解一元二次方程,解题的关键是:(1)按照等腰三角形的性质结合两点间的距离公式得出关于m的一元二次方程;(2)明白对称的性质以及到点的距离为定值的图象为圆.本题属于中档题,难度不大,(1)问题不大;(2)中巧用先寻找点P的对称的P′,再由对称去寻找点P.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案 如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在边CD上,连接DE,连接BG并延长交CD于点M,交DE于点H,则HM的长为$\frac{3\sqrt{5}}{5}$.
如图,在正方形ABCD和正方形CEFG中,AD=6,CE=2$\sqrt{2}$,点F在边CD上,连接DE,连接BG并延长交CD于点M,交DE于点H,则HM的长为$\frac{3\sqrt{5}}{5}$.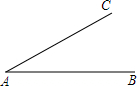 如图,线段AB和射线AC交于点A,∠A=30°,AB=20.点D在射线AC上,且∠ADB是钝角,写出一个满足条件的AD的长度值:AD=10.
如图,线段AB和射线AC交于点A,∠A=30°,AB=20.点D在射线AC上,且∠ADB是钝角,写出一个满足条件的AD的长度值:AD=10.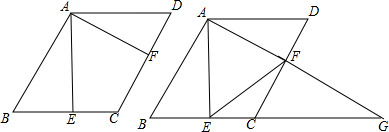
 如图,OP是∠MON内的一条射线,点A,B都在OP上,AC⊥OM,AD⊥ON,BE⊥OM、BF⊥ON,垂足分别为C,D,E,F,且AC=AD,求证:BE=BF.
如图,OP是∠MON内的一条射线,点A,B都在OP上,AC⊥OM,AD⊥ON,BE⊥OM、BF⊥ON,垂足分别为C,D,E,F,且AC=AD,求证:BE=BF.