题目内容
（a+b-2ab）（a+b-2）+（1-ab）2．
考点：因式分解
专题：
分析：重新分组进而将（a+b）看做整体，利用完全平方公式分解因式得出即可．
解答：解：（a+b-2ab）（a+b-2）+（1-ab）2
=[（a+b）-2ab][（a+b）-2]+（1-ab）2
=（a+b）2-2（ab+1）（a+b）+4ab+（1-ab）2
=（a+b）2-2（ab+1）（a+b）+[4ab+（1-ab）2]
=（a+b）-22（ab+1）（a+b）+（1+ab）2
=[（a+b）-（ab+1）]2
=[（a-1）（1-b）]2
=（a-1）2（b-1）2．
=[（a+b）-2ab][（a+b）-2]+（1-ab）2
=（a+b）2-2（ab+1）（a+b）+4ab+（1-ab）2
=（a+b）2-2（ab+1）（a+b）+[4ab+（1-ab）2]
=（a+b）-22（ab+1）（a+b）+（1+ab）2
=[（a+b）-（ab+1）]2
=[（a-1）（1-b）]2
=（a-1）2（b-1）2．
点评：此题主要考查了因式分解法的应用，熟练利用完全平方公式分解因式是解题关键．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图是一段楼梯，BC=2m，AB=4m．若在楼梯上铺地毯至少要（ ）| A、4m | B、6m | C、8m | D、10m |
如图，正方形ABCD中，E、F分别为BC、CD上的点，且AE⊥BF，垂足为点G．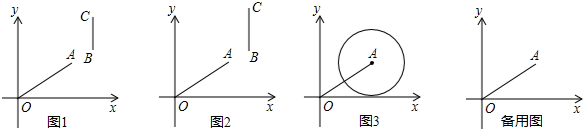
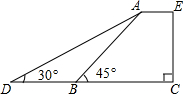如图是某滑板俱乐部训练时的斜坡截面的示意图，该截面垂直于水平面，出于安全因素考虑，俱乐部决定将训练的斜坡AB改造成AD，这时斜坡的坡角由45°降为30°，已知原斜坡面AB的长为6米，点D，B，C在同一水平直线上，AE∥DC，改善后斜坡坡面AD的长为多少米？
如图，在△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交DE的延长线于F点，连接CF．