题目内容
 如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF=
| 10 |
考点:平行四边形的判定与性质,勾股定理,三角形中位线定理
专题:
分析:(1)求出DE∥AB,AF∥BC来证明四边形ABDF是平行四边形.
(2)过点F作FG⊥AC于G点,求出AC和GF的长再求△CAF的面积.
(2)过点F作FG⊥AC于G点,求出AC和GF的长再求△CAF的面积.
解答:(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形;
(2)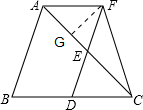
解:如图:过点F作FG⊥AC于G点,
∵BC=4,点D是边BC的中点,
∴BD=2,
由(1)可知四边形ABDF是平行四边形,
∴AF=BD=2,
∵∠CAF=45°,
∴AG=GF=
,
在Rt△FGC中,∠FGC=90°,GF=
,CF=
,
∴GC=
=2
,
∴AC=AG+GC=3
,
∴S△CAF=
AC•FG=
×3
×
=3.
∴DE∥AB,
∵AF∥BC,
∴四边形ABDF是平行四边形;
(2)

解:如图:过点F作FG⊥AC于G点,
∵BC=4,点D是边BC的中点,
∴BD=2,
由(1)可知四边形ABDF是平行四边形,
∴AF=BD=2,
∵∠CAF=45°,
∴AG=GF=
| 2 |
在Rt△FGC中,∠FGC=90°,GF=
| 2 |
| 10 |
∴GC=
| FC2-FG2 |
| 2 |
∴AC=AG+GC=3
| 2 |
∴S△CAF=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查了平行四边形的判定及平行四边形的性质,解题的过程中勾股定理的运用很关键.

练习册系列答案
相关题目
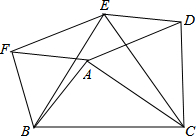 已知,如图,△ABF,△ACD,△BCE都是等边三角形,求证:四边形ADEF是平行四边形.
已知,如图,△ABF,△ACD,△BCE都是等边三角形,求证:四边形ADEF是平行四边形.
 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,求证:AE=EF+BF.
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB上一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,求证:AE=EF+BF.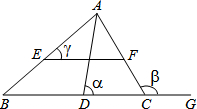 如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则:
如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则: