题目内容
下列图形中不是轴对称而是中心对称图形的是( )
A. 等边三角形
B. 平行四边形
C. 矩形
D. 菱形
 B
【解析】试题解析:等边三角形不是中心对称图形,对称轴为三条中线所在直线;平行四边形的对称中心为两条对角线的交点,不是轴对称图形;矩形的对称中心为两条对角线的交点,对称轴为两对边中点连线所在直线;菱形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线;所以选择B.
B
【解析】试题解析:等边三角形不是中心对称图形,对称轴为三条中线所在直线;平行四边形的对称中心为两条对角线的交点,不是轴对称图形;矩形的对称中心为两条对角线的交点,对称轴为两对边中点连线所在直线;菱形的对称中心为两条对角线的交点,对称轴为两条对角线所在直线;所以选择B.
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
从一副扑克牌中任取一张,则抽到红桃的频率与抽到黑桃的频率哪个大?抽到梅花与抽到大、小王的频率哪个大?
 抽到红桃的可能性与抽到黑桃的频率一样大,而抽到梅花的频率大于抽到大、小王的频率.
【解析】试题分析: 本题考察可能性大小的应用,关键是根据各色扑克的张数求出各色扑克被抽到的频率是多少.
【解析】
一副扑克牌有54张,其中红桃、黑桃、梅花、方块各13张,大、小王各一张,所以,抽到红桃的的频率为,抽到黑桃的的频率为,抽到梅花的的频率为,抽到大、小王的的频率为. 所以抽到红桃的可能性与抽到...
抽到红桃的可能性与抽到黑桃的频率一样大,而抽到梅花的频率大于抽到大、小王的频率.
【解析】试题分析: 本题考察可能性大小的应用,关键是根据各色扑克的张数求出各色扑克被抽到的频率是多少.
【解析】
一副扑克牌有54张,其中红桃、黑桃、梅花、方块各13张,大、小王各一张,所以,抽到红桃的的频率为,抽到黑桃的的频率为,抽到梅花的的频率为,抽到大、小王的的频率为. 所以抽到红桃的可能性与抽到... 在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B等于_____.
 6种
【解析】试题分析:当△ABC是锐角三角形时,则∠B=70°,当△ABC是钝角三角形时,则∠B=20°.
6种
【解析】试题分析:当△ABC是锐角三角形时,则∠B=70°,当△ABC是钝角三角形时,则∠B=20°. 关于中心对称的两个图形,对称点的连线经过__________
 对称中心
【解析】关于中心对称的两个图形,对称点的连线经过对称中心.
故答案:对称中心.
对称中心
【解析】关于中心对称的两个图形,对称点的连线经过对称中心.
故答案:对称中心. △ABC和△AˊBˊCˊ关于点O对称,下列结论不正确的是( )
A. AO=AˊO
B. AB∥AˊBˊ
C. CO=BO
D. ∠BAC=∠BˊAˊCˊ
 C
【解析】因为只有对称点到对称中心的距离相等,所以C选项是错误的
故选C.
C
【解析】因为只有对称点到对称中心的距离相等,所以C选项是错误的
故选C. 分解因式:
(1)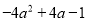 (2)
(2) 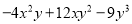
(3)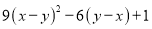 (4)
(4) 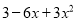
(5)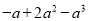 (6)
(6) 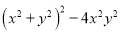
(7)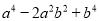 8)
8)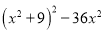
(9)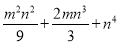 (10)
(10)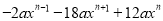
 (1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
...
(1)-(2a-1)2;(2)-y(2x-3y)2;(3)(3x-3y+1)2;(4)3(1-x)2;(5)-a(1-a)2;
(6)(x+y)2(x-y)2; (7)(a+b)2(a-b)2; (8)(x+3)2(x-3)2; (9) ;(10) .
【解析】试题分析:(1)首先提取负号,再利用完全平方公式进行分解;
(2)首先提取公因式-y,再利用完全平方公式进行分解;
... 已知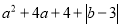 =0,则a+b=__________.
=0,则a+b=__________.
 1
【解析】∵a2+4a+4+|b-3|=0,∴(a+2)2+|b-3|=0,∴a+2=0,b-3=0,∴a=-2,b=3,∴a+b=1,
故答案为:1.
1
【解析】∵a2+4a+4+|b-3|=0,∴(a+2)2+|b-3|=0,∴a+2=0,b-3=0,∴a=-2,b=3,∴a+b=1,
故答案为:1. 已知点A(﹣1,﹣2),点B(1,4)
(1)试建立相应的平面直角坐标系;
(2)描出线段AB的中点C,并写出其坐标;
(3)将线段AB沿水平方向向右平移3个单位长度得到线段A1B1,写出线段A1B1两个端点及线段中点C1的坐标.
 (1)见解析;(2)C(0,1);(3)平移规律是(x+3,y),所以A1(2,﹣2),B1(4,4),C1(3,1).
【解析】试题分析:画出平面直角坐标系后描出线段AB的中点C,根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1(2,﹣2),B1(4,4),C1(3,1).
试题解析:【解析】
(1)坐标系如图:
(2)C(0,1);
(3)平移规律是(...
(1)见解析;(2)C(0,1);(3)平移规律是(x+3,y),所以A1(2,﹣2),B1(4,4),C1(3,1).
【解析】试题分析:画出平面直角坐标系后描出线段AB的中点C,根据平移的规律求出线段A1B1两个端点及线段中点C1的坐标为A1(2,﹣2),B1(4,4),C1(3,1).
试题解析:【解析】
(1)坐标系如图:
(2)C(0,1);
(3)平移规律是(... 二次函数y=ax2+bx的图象如图,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
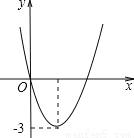
A. -3 B. 3 C. -6 D. 9
 B
【解析】先根据抛物线的开口向上可知a>0,由顶点纵坐标为-3得出b与a关系,再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式,求出m的取值范围即可.
【解析】
∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0, =-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3...
B
【解析】先根据抛物线的开口向上可知a>0,由顶点纵坐标为-3得出b与a关系,再根据一元二次方程ax2+bx+m=0有实数根可得到关于m的不等式,求出m的取值范围即可.
【解析】
∵抛物线的开口向上,顶点纵坐标为-3,
∴a>0, =-3,即b2=12a,
∵一元二次方程ax2+bx+m=0有实数根,
∴△=b2-4am≥0,即12a-4am≥0,即12-4m≥0,解得m≤3... 
