题目内容
2.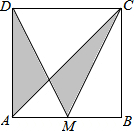 如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
分析 根据正方形的性质可得到△AME∽△CDE,根据相似三角形的边对应边成比例,求得EH,EF的长,从而即可求得阴影部分的面积.
解答 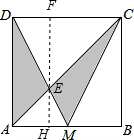 解:如图,过点E作HF⊥AB
解:如图,过点E作HF⊥AB
∵AM∥CD,
∴∠DCE=∠EAM,∠CDE=∠EMA,
∴△AME∽△CDE
∴AM:DC=EH:EF=1:2,FH=AD=1
∴EH=$\frac{1}{3}$,EF=$\frac{2}{3}$.
∴阴影部分的面积=S正-S△AME-S△CDE-S△MBC=1-$\frac{1}{12}$-$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{3}$.
故选B.
点评 本题考查了正方形的性质,相似三角形的判定和性质,找出各线段之间的比例关系是本题解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
11.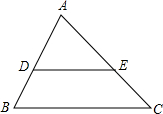 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
 如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )
如图,已知点D、E在△ABC的边上,DE∥BC,∠B=60°,∠AED=40°,则∠A的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
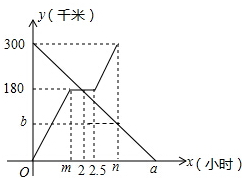 甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息1小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途经C地时休息1小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.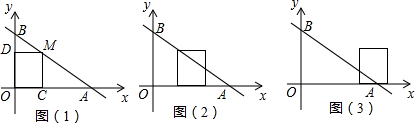
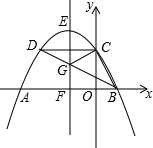 如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.
如图,抛物线y=ax2+bx+4交y轴于点C,交x轴于点A,B(A在B的左边),顶点为E,对称轴直线EF交x轴于点F,CD∥x轴交抛物线于点D,连结BD交EF于点G.若点B(2,0),且△BCG恰为直角三角形,则EF的长为$\frac{25}{4}$.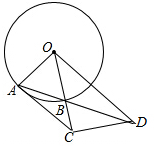 已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.
已知⊙O的半径OA=3,B为⊙O上一点,延长OB,在OB延长线上截取一点C,使得BC=2,CD垂直于BC交AB延长线于点D,连接AC,若AC=CD,则AB=$\frac{6\sqrt{5}}{5}$.