题目内容
10.解方程$\frac{1}{2}${x-$\frac{1}{2}$[x-$\frac{1}{4}$(x-$\frac{2}{3}$)-$\frac{3}{2}$]}=x+$\frac{3}{4}$.分析 去括号、去分母、移项、合并同类项、系数化为1,
解答 解:$\frac{1}{2}${x-$\frac{1}{2}$[x-$\frac{1}{4}$(x-$\frac{2}{3}$)-$\frac{3}{2}$]}=x+$\frac{3}{4}$,
x-$\frac{1}{2}$[x-$\frac{1}{4}$(x-$\frac{2}{3}$)-$\frac{3}{2}$]=2x+$\frac{3}{2}$,
-$\frac{1}{2}$[x-$\frac{1}{4}$(x-$\frac{2}{3}$)-$\frac{3}{2}$]=x+$\frac{3}{2}$,
x-$\frac{1}{4}$(x-$\frac{2}{3}$)-$\frac{3}{2}$=-2x-3,
x-$\frac{1}{4}$x+$\frac{1}{6}$-$\frac{3}{2}$=-2x-3,
12x-3x+2-18=-24x-36,
33x=-20,
x=-$\frac{20}{33}$.
点评 考查了解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.

练习册系列答案
相关题目
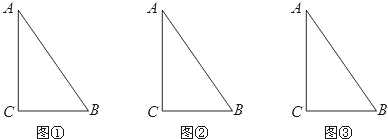
5. 如图,已知△ABC,△DCE是两个全等的等腰三角形,底边BC、CE在同一直线上,且AB=$\sqrt{2}$,BC=1,BD与AC交于点P.
如图,已知△ABC,△DCE是两个全等的等腰三角形,底边BC、CE在同一直线上,且AB=$\sqrt{2}$,BC=1,BD与AC交于点P.
(1)求证:△BED∽△DEC;
(2)求△DPC的周长.
 如图,已知△ABC,△DCE是两个全等的等腰三角形,底边BC、CE在同一直线上,且AB=$\sqrt{2}$,BC=1,BD与AC交于点P.
如图,已知△ABC,△DCE是两个全等的等腰三角形,底边BC、CE在同一直线上,且AB=$\sqrt{2}$,BC=1,BD与AC交于点P.(1)求证:△BED∽△DEC;
(2)求△DPC的周长.
20.如果一个角的补角是110°,则这个角的余角的度数是( )
| A. | 30° | B. | 20° | C. | 70° | D. | 110° |
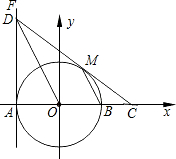 如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A,B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.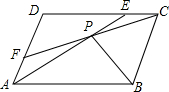 ?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.
?ABCD中,E、F分别是CD、AD边上的点,且AE=CF,AE,CF交于点P,求证:PB平分∠APC.