��Ŀ����
�ı���ABCD�У�E�DZ�AB��һ�㣨�����A��B�غϣ�������ED��EC�����ı���ABCD�ֳ����������Σ����������������������ƣ����E�����ı���ABCD�ı�AB�ϵ����Ƶ㣻�������������ζ����ƣ����E�����ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣮
��1����ͼ�٣���A=��B=��DEC=60�㣬���жϵ�E�Ƿ�Ϊ�ı���ABCD�ı�AB�ϵ����Ƶ㣿��˵�����ɣ�
��2����ͼ�ڣ��ڣ�1���������£���E��AB���е㣬
���жϵ�E�Ƿ�Ϊ�ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣿��˵�����ɣ�
����AD•BC=18����AB�ij���
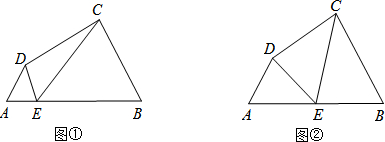
��3���ھ���ABCD�У�AB=10��BC=3����A��B��C��D�ĵ��������������������ÿ��С�����εı߳�Ϊ1���ĸ���ϣ�����ͼ���л�������ABCD�ı�AB�ϵ�һ���ƽ����Ƶ�E��

��1����ͼ�٣���A=��B=��DEC=60�㣬���жϵ�E�Ƿ�Ϊ�ı���ABCD�ı�AB�ϵ����Ƶ㣿��˵�����ɣ�
��2����ͼ�ڣ��ڣ�1���������£���E��AB���е㣬
���жϵ�E�Ƿ�Ϊ�ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣿��˵�����ɣ�
����AD•BC=18����AB�ij���

��3���ھ���ABCD�У�AB=10��BC=3����A��B��C��D�ĵ��������������������ÿ��С�����εı߳�Ϊ1���ĸ���ϣ�����ͼ���л�������ABCD�ı�AB�ϵ�һ���ƽ����Ƶ�E��

���㣺�������ۺ���,���ε�����,���������ε��ж�������
ר�⣺�¶���
��������1����������A=��B=��DEC=60��ɵá�BEC=��ADE���Ӷ��õ���AED�ס�BCE���ʵ�E���ı���ABCD�ı�AB�ϵ����Ƶ㣮
��2�����ɡ�AED�ס�BCE�ɵ�
=
=
����E��AB���е�ɵ�AE=BE���Ӷ��õ�
=
����������֤����AED�ס�ECD���ʵ�E���ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣮�ڸ���
=
��AE=BE=
AB��AD•BC=18�Ϳ����AB�ij���
��3����AE=1��BE=1ʱ������֤����EBC�ס�DAE����DAE�ס�CED���Ӷ��õ���E�Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣮
��2�����ɡ�AED�ס�BCE�ɵ�
| AD |
| BE |
| AE |
| BC |
| ED |
| CE |
| AD |
| AE |
| ED |
| CE |
| AD |
| BE |
| AE |
| BC |
| 1 |
| 2 |
��3����AE=1��BE=1ʱ������֤����EBC�ס�DAE����DAE�ס�CED���Ӷ��õ���E�Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣮
����⣺��1����E���ı���ABCD�ı�AB�ϵ����Ƶ㣮
֤������ͼ�٣�

�ߡ�A=��B=��DEC=60�㣬��DEB=��A+��ADE��
���BEC+60��=60��+��ADE��
���BEC=��ADE��
���AED�ס�BCE��
���E���ı���ABCD�ı�AB�ϵ����Ƶ㣮
��2����ͼ�ڣ�
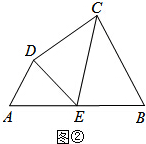
�ٵ�E���ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣮
֤�����ɣ�1���á�AED�ס�BCE��
����
=
=
��
��E��AB���е㣬
��AE=BE=
AB��
��
=
��
�ߡ�A=��DEC��
���AED�ס�ECD��
���AED�ס�BCE�ס�ECD��
���E���ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣮
�ڡ�
=
����֤����
��AD•BC=AE•BE��
��AD•BC=18��AE=BE=
AB��
��18=��
AB��2��
��AB=6
��
��AB�ij�Ϊ6
��
��3������AB��ȡһ��E��ʹ��AE=1����E���Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣬��ͼ�ۣ�
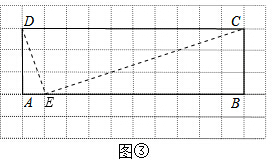
�������£�
����DE��CE��
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬AD=BC��
��AB=10��BC=3��AE=1��
��EB=9��AD=3��
��
=3=
��
���EBC�ס�DAE��
��
=
����BEC=��ADE��
��AD=BC��
��
=
��
�ߡ�A=90�㣬
���ADE+��AED=90�㣮
���BEC+��AED=90�㣮
���DEC=90�㣮
���A=��DEC��
���DAE�ס�CED��
���EBC�ס�DAE�ס�CED��
���E�Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣮
����AB��ȡһ��E��ʹ��BE=1����E���Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣬��ͼ�ۡ䣬
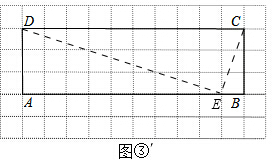
�������£�
����DE��CE��
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬AD=BC��
��AB=10��BC=3��BE=1��
��AE=9��AD=3��
��
=
=
��
���EBC�ס�DAE��
��
=
����BEC=��ADE��
��AD=BC��
��
=
��
�ߡ�A=90�㣬
���ADE+��AED=90�㣮
���BEC+��AED=90�㣮
���DEC=90�㣮
���A=��DEC��
���DAE�ס�CED��
���EBC�ס�DAE�ס�CED��
���E�Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣮
֤������ͼ�٣�

�ߡ�A=��B=��DEC=60�㣬��DEB=��A+��ADE��
���BEC+60��=60��+��ADE��
���BEC=��ADE��
���AED�ס�BCE��
���E���ı���ABCD�ı�AB�ϵ����Ƶ㣮
��2����ͼ�ڣ�

�ٵ�E���ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣮
֤�����ɣ�1���á�AED�ס�BCE��
����
| AD |
| BE |
| AE |
| BC |
| ED |
| CE |
��E��AB���е㣬
��AE=BE=
| 1 |
| 2 |
��
| AD |
| AE |
| ED |
| CE |
�ߡ�A=��DEC��
���AED�ס�ECD��
���AED�ס�BCE�ס�ECD��
���E���ı���ABCD�ı�AB�ϵĻƽ����Ƶ㣮
�ڡ�
| AD |
| BE |
| AE |
| BC |
��AD•BC=AE•BE��
��AD•BC=18��AE=BE=
| 1 |
| 2 |
��18=��
| 1 |
| 2 |
��AB=6
| 2 |
��AB�ij�Ϊ6
| 2 |
��3������AB��ȡһ��E��ʹ��AE=1����E���Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣬��ͼ�ۣ�

�������£�
����DE��CE��
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬AD=BC��
��AB=10��BC=3��AE=1��
��EB=9��AD=3��
��
| EB |
| BC |
| AD |
| AE |
���EBC�ס�DAE��
��
| EC |
| DE |
| BC |
| AE |
��AD=BC��
��
| EC |
| DE |
| AD |
| AE |
�ߡ�A=90�㣬
���ADE+��AED=90�㣮
���BEC+��AED=90�㣮
���DEC=90�㣮
���A=��DEC��
���DAE�ס�CED��
���EBC�ס�DAE�ס�CED��
���E�Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣮
����AB��ȡһ��E��ʹ��BE=1����E���Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣬��ͼ�ۡ䣬

�������£�
����DE��CE��
���ı���ABCD�Ǿ��Σ�
���A=��B=90�㣬AD=BC��
��AB=10��BC=3��BE=1��
��AE=9��AD=3��
��
| EB |
| BC |
| 1 |
| 3 |
| AD |
| AE |
���EBC�ס�DAE��
��
| EC |
| DE |
| BC |
| AE |
��AD=BC��
��
| EC |
| DE |
| AD |
| AE |
�ߡ�A=90�㣬
���ADE+��AED=90�㣮
���BEC+��AED=90�㣮
���DEC=90�㣮
���A=��DEC��
���DAE�ס�CED��
���EBC�ס�DAE�ס�CED��
���E�Ǿ���ABCD�ı�AB�ϵ�һ���ƽ����Ƶ㣮
�������������¶����¿��������������ε��ж������ʡ����ε����ʵ�֪ʶ���������˲����������Ķ�����������̽������������һ������������ĺ��⣮

��ϰ��ϵ�д�
�����Ŀ
Ϊ���˽�ijУ���꼶260�����������������������������30�������������ǵ����߽���ͳ�Ʒ�����������
30���������ߵ�ƽ������160cm�����н����в���ȷ�ǣ�������
30���������ߵ�ƽ������160cm�����н����в���ȷ�ǣ�������
| A��260������������������ |
| B����ȡ��30�������������������һ������ |
| C��������260���������ߵ�ƽ����һ����160cm |
| D������������30 |