题目内容
14.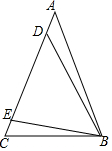 如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.
如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.
分析 设∠A=α,∠ABD=∠CBE=β,由三角形外角的性质得到∠BDE=∠A+∠ABD,于是得到∠BDE=α+β,根据等腰三角形的性质得到∠EBD=∠BDE=α+β,根据三角形的内角和列方程α+α+3β+α+3β=180°,得到∠DBC=60°,过C作CF⊥BD于F,解直角三角形即可得到结论.
解答 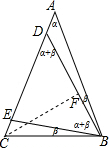 解:设∠A=α,∠ABD=∠CBE=β,
解:设∠A=α,∠ABD=∠CBE=β,
∵∠BDE=∠A+∠ABD,
∴∠BDE=α+β,
∵BE=DE,
∴∠EBD=∠BDE=α+β,
∴∠ABC=β+α+β+β=3β+α,
∵AB=AC,
∴∠C=∠ABC=α+3β,
∴α+α+3β+α+3β=180°,
∴α+2β=60°,
∴∠DBC=60°,
过C作CF⊥BD于F,
∴∠FCB=30°,
∴CF=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查了等腰三角形的性质,三角形的内角和,三角形的外角的性质,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA,求∠ADE的度数.
如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA,求∠ADE的度数.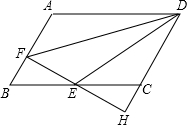 如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H.
如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H.