题目内容
9. 如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA,求∠ADE的度数.
如图,在△ABC中,∠BAC=90°,∠B=56°,AD⊥BC,DE∥CA,求∠ADE的度数.
分析 根据平行线的性质推知△AED是直角三角形;在直角△ABD中,利用“直角三角形的两个锐角互余的性质”求得∠BAD=34°;然后在直角△AED中,利用“直角三角形的两个锐角互余的性质”求得∠ADE的度数.
解答 解:∵∠BAC=90°,DE∥AC(已知)
∴∠DEA=180°-∠BAC=90°(两直线平行,同旁内角互补).
∵AD⊥BC,∠B=56°,
∴∠BAD=34°,
在△ADE中,∵DE⊥AB,
∴∠ADE=56°.
点评 本题考查了三角形内角和定理以及平行线的性质,直角三角形的性质.直角三角形的两个锐角互余,此题难度不大.

练习册系列答案
相关题目
20.高度每增加1千米,气温就下降2℃,现在地面气温是-10℃,那么离地面高度为7千米的高空的气温是( )
| A. | -4℃ | B. | -14℃ | C. | -24℃ | D. | 14℃ |
 蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为4m.
蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为4m.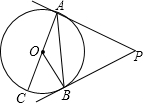 如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35°,求∠P的度数.
如图,PA、PB是⊙O的两条切线,A、B是切点,AC是⊙O的直径,∠BAC=35°,求∠P的度数.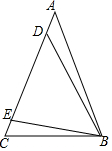 如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.
如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$. 如图,Rt△ABC的顶点B在反比例函数y=$\frac{12}{x}$的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是12-$\frac{3}{2}$$\sqrt{3}$.
如图,Rt△ABC的顶点B在反比例函数y=$\frac{12}{x}$的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是12-$\frac{3}{2}$$\sqrt{3}$. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.