题目内容
4.若二次函数y=x2-x-2的函数值小于0,则x的取值范围是-1<x<2.分析 根据函数解析式可以确定图象与x轴的交点是(-1,0),(2,0),又当y<0时,图象在x轴的下方,由此可以确定x的取值范围.
解答 解:当y=0时,即x2-x-2=0,
∴x1=-1,x2=2,
∴图象与x轴的交点是(-1,0),(2,0),
当y<0时,图象在x轴的下方,
此时-1<x<2.
故填空答案:-1<x<2.
点评 本题考查了抛物线和x轴交点的问题,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y<0时,自变量x的范围,锻炼了学生数形结合的思想方法.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
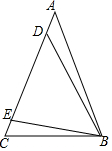 如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.
如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$. 如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.
如图所示,小华从点A出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A时,走的路程一共是150米.