题目内容
6.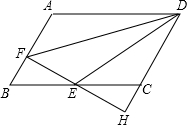 如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H.
如图,在?ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H.(1)求证:△BEF≌△CEH;
(2)求DE的长.
分析 (1)由平行四边形的性质得出AB∥CD,由AAS证明△BEF≌△CEH即可;
(2)由平行四边形的性质得出CD=AB=3,BC=AD=4,AB∥CD,由平行线的性质得出∠HCE=∠B=60°,证出EF⊥DH,由含30°角的直角三角形的性质得出CH=$\frac{1}{2}$CE=1,求出EH=$\sqrt{3}$CG=$\sqrt{3}$,DH=CD+CH=4,由勾股定理求出DE即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵EF⊥AB∴EF⊥CD,∴∠BFE=∠CHE=90°,
∵E是BC的中点,
∴BE=CE,
在△BEF和△CEH中,$\left\{\begin{array}{l}{∠BFE=∠CHE}&{\;}\\{∠BEF=∠CEH}&{\;}\\{BE=CE}&{\;}\end{array}\right.$,
∴△BEF≌△CEH(AAS);
(2)解:∵EF⊥AB,∠ABC=60°,BE=$\frac{1}{2}$BC=$\frac{1}{2}$AD=2.
∴BF=1,EF=$\sqrt{3}$.
∵△BEF≌△CEH,
∴BF=CH=1,EF=EH=$\sqrt{3}$,DH=4,
∵∠CHE=90°,
∴DE2=EH2+DH2.
∴DE=$\sqrt{3+16}$=$\sqrt{19}$.
点评 本题考查了平行四边形的性质、含30°角的直角三角形的性质、勾股定理;熟练掌握平行四边形的性质,由含30°角的直角三角形的性质求出CG是解决问题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
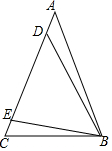 如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.
如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.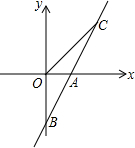 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2). 如图,Rt△ABC的顶点B在反比例函数y=$\frac{12}{x}$的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是12-$\frac{3}{2}$$\sqrt{3}$.
如图,Rt△ABC的顶点B在反比例函数y=$\frac{12}{x}$的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是12-$\frac{3}{2}$$\sqrt{3}$.