题目内容
4.当a≥-$\frac{5}{2}$时,式子$\frac{2a+5}{|a|+1}$的值不小于0.分析 根据式子的值不小于0,求出a的范围即可.
解答 解:由题意得:$\frac{2a+5}{|a|+1}$≥0,
∵|a|≥0,
∴|a|+1≥1>0,
∴2a+5≥0,
解得:a≥-$\frac{5}{2}$,
故答案为:≥-$\frac{5}{2}$
点评 此题考查了分式的值,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.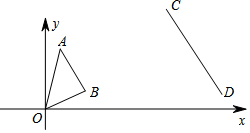 如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
 如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )| A. | (0,0) | B. | (3,4)或(-6,2) | C. | (5,3)或(-7,1) | D. | 不能确定 |
12.下列说法正确的是( )
| A. | -$\frac{2mn}{3}$的系数是-2 | B. | 32ab3的次数是6次 | ||
| C. | x2+x-1的常数项为1 | D. | 4x2y-5x2y2+7xy是四次三项式 |
 如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下: 蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为4m.
蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为4m. 如图是有一些完全相同的小正方体搭成的几何体分别从左面和上面看到的形状图,搭成这个几何体最多需要8个小正方体.
如图是有一些完全相同的小正方体搭成的几何体分别从左面和上面看到的形状图,搭成这个几何体最多需要8个小正方体.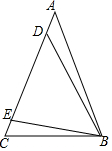 如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.
如图,在三角形ABC中,AB=AC,∠ABD=∠CBE,BE=DE,若BC=1,则点C到BD所在直线的距离为$\frac{\sqrt{3}}{2}$.