题目内容
5.在Rt△ABC中,∠ACB=90°,tan∠BAC=$\frac{1}{2}$,点D在边AC上且AD=$\frac{1}{4}$AC,连结BD,F为BD中点,若BC=6,将线段AD绕点A旋转一周,点F始终为BD中点,求点F运动路径的长度.分析 根据锐角三角函数,可得AC的长,根据三角形中线的性质,可得EF的长,ED的长,根据勾股定理,可得AF的长,根据圆的周长公式,可得答案.
解答 解:如图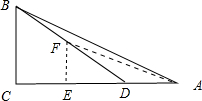 ,
,
作FE∥BC,交AC于E,
由,∠ACB=90°,tan∠BAC=$\frac{1}{2}$,若BC=6,得
AC=2AC=12.
由点D在边AC上且AD=$\frac{1}{4}$AC,得
AD=3,CD=12-3=9.
由FE∥BC,BC=6,CD=9,得
FE=$\frac{1}{2}$BC=3,CE=DE=$\frac{1}{2}$CD=$\frac{9}{2}$,∠FED=90°.
在Rt△AEF中,由勾股定理,得
AF=$\sqrt{E{F}^{2}+A{E}^{2}}$=$\sqrt{{3}^{2}+(3+\frac{9}{2})^{2}}$=$\frac{\sqrt{261}}{2}$,
由线段AD绕点A旋转一周,得
AF绕A点旋转一周,即F点的轨迹是以A点为圆心的圆,
点F运动路径的长度2πr=2π×$\frac{\sqrt{261}}{2}$=$\sqrt{261}$π.
点评 本题考查了轨迹,利用三角形的中位线得出EF的长,ED的长是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.Rt△ABC的两边长分别为3和4,则第三边长的平方是( )
| A. | 25 | B. | 7 | C. | 12 | D. | 25或7 |
10.下列计算正确的是( )
| A. | a2+a2=2a4 | B. | (-a2b)3=-a6b3 | C. | a2•a4=a4 | D. | a4÷a2=a4 |
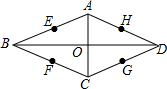 如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AB、BC、CD、DA的中点,点E、F、G、H在以点O为圆心的同一个圆上吗?为什么?
如图,菱形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AB、BC、CD、DA的中点,点E、F、G、H在以点O为圆心的同一个圆上吗?为什么?
 如图,已知BC=EC,∠BCE=∠ACD,要使△BCA≌△ECD,则应添加的一个条件为AC=CD.(答案不唯一,只需填一个)
如图,已知BC=EC,∠BCE=∠ACD,要使△BCA≌△ECD,则应添加的一个条件为AC=CD.(答案不唯一,只需填一个)