题目内容
7.已知二次函数y=2(x-6)2的图象与y轴交于A点,它的顶点是B,坐标系的原点是O,求△AOB的面积.分析 可先求得A、B的坐标,再利用三角形面积容易求得△AOB的面积.
解答 解:
∵y=2(x-6)2=2x2-24x+72,
∴B(6,0),A(0,72),
∴AO=72,BO=6,
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×72×6=216.
点评 本题主要考查二次函数的性质,由解析式求得A、B两点的坐标是解题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
15.下列判断中,你认为正确的是( )
| A. | 0的立方根是0 | B. | $\root{3}{27}$是无理数 | C. | 4的平方根是2 | D. | -1没有立方根 |
 如图,∠A=∠C=90°,BE,DF分别为∠ABC与∠ADC的平分线,能判断BE∥DF吗?试说明理由.
如图,∠A=∠C=90°,BE,DF分别为∠ABC与∠ADC的平分线,能判断BE∥DF吗?试说明理由.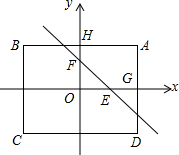 如图,已知矩形ABCD的面积为48,以此矩形的对称轴为坐标轴建立直角坐标系.设A(x,y),其中x>0,y>0.
如图,已知矩形ABCD的面积为48,以此矩形的对称轴为坐标轴建立直角坐标系.设A(x,y),其中x>0,y>0. 如图所示,在图中请以AB所在直线为对称轴,画出已知图形的对称图形.
如图所示,在图中请以AB所在直线为对称轴,画出已知图形的对称图形.