题目内容
7.计算:(1)$\sqrt{2}$sin45°+sin30°•cos60°;
(2)$\sqrt{4}$+($\frac{1}{2}$)-1-2cos60°+(2-π)0.
(3)$\sqrt{2}$+1-3tan230°+2$\sqrt{(sin45°-1)^{2}}$.
分析 (1)原式利用特殊角的三角函数值计算即可得到结果;
(2)原式第一项利用算术平方根定义计算,第二项利用负整数指数幂法则计算,第三项利用特殊角的三角函数值计算,最后一项利用零指数幂法则计算即可得到结果;
(3)原式利用特殊角的三角函数值及二次根式性质计算即可得到结果.
解答 解:(1)原式=$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$×$\frac{1}{2}$=1$\frac{1}{4}$;
(2)原式=2+2-2×$\frac{1}{2}$+1=4-1+1=4;
(3)原式=$\sqrt{2}$+1-3×$\frac{1}{3}$+2×(1-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$+1-1+2-$\sqrt{2}$=2.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
17. 线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )
线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )
 线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )
线段AB、CD在平面直角坐标系中的位置如图所示,O为坐标原点.若线段AB上一点P的坐标为(3.5,2),则直线OP与线段CD的交点的坐标为( )| A. | (7,2) | B. | (3.5,4) | C. | (3.5,2) | D. | (7,4) |
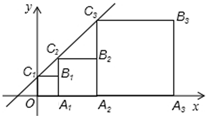 正方形OA1B1C1、正方形A1A2B2C2和正方形A2A3B3C3按如图所示方式放置,点C1、C2、C3在直线y=x+1上,点A1、A2、A3在x轴上,已知C1点的坐标是(0,1),则B3的坐标为(7,4).
正方形OA1B1C1、正方形A1A2B2C2和正方形A2A3B3C3按如图所示方式放置,点C1、C2、C3在直线y=x+1上,点A1、A2、A3在x轴上,已知C1点的坐标是(0,1),则B3的坐标为(7,4). 如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?
如图,AB∥CD,AB=CD,∠A=∠C.你能得到哪些有关角、边的结论?△ABF与△CDE全等吗?