题目内容
 如图,已知AC⊥CB,D、E分别为AC、CB的中点,且CD=CE=15,则△BEG的面积为( )
如图,已知AC⊥CB,D、E分别为AC、CB的中点,且CD=CE=15,则△BEG的面积为( )| A、50 | B、60 | C、75 | D、90 |
考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:
分析:如图,连接DE、AB.根据三角形的面积公式以及图形推知S△ACE=S△BCD,S△AGB=S四边形CDGE.然后由三角形中位线的性质、相似三角形△DEG∽△BAG的面积的比等于相似比的平方证得
S△BAG=4S△DGE,最后利用“分割法”知S△DCE+S△DGE+S△AGB+S△ADG+S△BEG=S△DCE+
S△DCE+
S△DCE+2S△BEG=S△ABC,即2S△BEG=S△ABC-
S△DCE=150.
S△BAG=4S△DGE,最后利用“分割法”知S△DCE+S△DGE+S△AGB+S△ADG+S△BEG=S△DCE+
| 1 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
解答: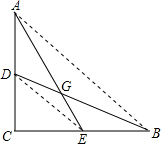 解:如图,连接DE、AB.
解:如图,连接DE、AB.
∵D、E分别为AC、CB的中点,且CD=CE,
∴AC=2CD,BC=2CE.
又∵AC⊥CB,
∴S△ACE=
CE•AC=
×CE•2CD=CE•CD,S△BCD=
CD•BC=
×CD•2CE=CE•CD,
∴S△ACE=S△BCD,
∴S△ACE-S四边形CDGE=S△BCD-S四边形CDGE,即S△ADG=S△BEG.
又∵S△AEB=S△ACE(等底同高的两个三角形的面积相等),
∴S△AGB=S四边形CDGE.
∵D、E分别为AC、CB的中点,
∴DE∥AB,
=
,
∴△DEG∽△BAG,
∴
=(
)2=
,
∴S△BAG=4S△DGE,
∴
S△DCE=S△DGE.
∴S△DCE+S△DGE+S△AGB+S△ADG+S△BEG=S△DCE+
S△DCE+
S△DCE+2S△BEG=S△ABC,即2S△BEG=S△ABC-
S△DCE=
×2CE•2CD-
×
×CD•CE=
×15×15=150,
则S△BEG=75.
故选C.
 解:如图,连接DE、AB.
解:如图,连接DE、AB.∵D、E分别为AC、CB的中点,且CD=CE,
∴AC=2CD,BC=2CE.
又∵AC⊥CB,
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ACE=S△BCD,
∴S△ACE-S四边形CDGE=S△BCD-S四边形CDGE,即S△ADG=S△BEG.
又∵S△AEB=S△ACE(等底同高的两个三角形的面积相等),
∴S△AGB=S四边形CDGE.
∵D、E分别为AC、CB的中点,
∴DE∥AB,
| DE |
| AB |
| 1 |
| 2 |
∴△DEG∽△BAG,
∴
| S△DEG |
| S△BAG |
| DE |
| AB |
| 1 |
| 4 |
∴S△BAG=4S△DGE,
∴
| 1 |
| 3 |
∴S△DCE+S△DGE+S△AGB+S△ADG+S△BEG=S△DCE+
| 1 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
则S△BEG=75.
故选C.
点评:本题考查了相似三角形的判定与性质.解答该题时,注意利用“分割法”来求△BEG的面积.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,在长方形ABCD中,E、F分别是边BC、CD上的点,已知S△ABE=5,S△AFD=7,S△AEF=15.5,求长方形ABCD的面积.
如图,在长方形ABCD中,E、F分别是边BC、CD上的点,已知S△ABE=5,S△AFD=7,S△AEF=15.5,求长方形ABCD的面积.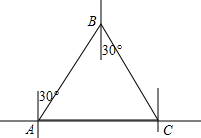 海上有两个观测站A、B,测得B站在A站AB=30海里.一艘船C,在A站的正东,在B站的南偏东30°处.此时船正向正北方向航行,半小时后达到D处,此时测得船在A站北偏东60°方向,在B站南偏东75°方向.
海上有两个观测站A、B,测得B站在A站AB=30海里.一艘船C,在A站的正东,在B站的南偏东30°处.此时船正向正北方向航行,半小时后达到D处,此时测得船在A站北偏东60°方向,在B站南偏东75°方向. 如图,已知圆锥的底面圆直径AB为2r(r>0),母线长OA为3r,C为母线OB的中点,在圆锥的侧面上,一只蚂蚁从点A爬行到点C的最短路线长为
如图,已知圆锥的底面圆直径AB为2r(r>0),母线长OA为3r,C为母线OB的中点,在圆锥的侧面上,一只蚂蚁从点A爬行到点C的最短路线长为