题目内容
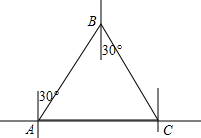 海上有两个观测站A、B,测得B站在A站AB=30海里.一艘船C,在A站的正东,在B站的南偏东30°处.此时船正向正北方向航行,半小时后达到D处,此时测得船在A站北偏东60°方向,在B站南偏东75°方向.
海上有两个观测站A、B,测得B站在A站AB=30海里.一艘船C,在A站的正东,在B站的南偏东30°处.此时船正向正北方向航行,半小时后达到D处,此时测得船在A站北偏东60°方向,在B站南偏东75°方向.(1)试画出D点的位置并求船航行的速度;
(2)求BD的长度.
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)首先根据题意作图,然后由题意可证得△ABC是等边三角形,然后在Rt△ACD中,利用三角函数的知识即可求得CD的长;
(2)首先过点D作DH⊥BC于点H,由题意可求得∠DBH=45°,∠DCH=30°,然后分别在Rt△CDH和Rt△BDH中,利用三角函数的知识即可求得答案.
(2)首先过点D作DH⊥BC于点H,由题意可求得∠DBH=45°,∠DCH=30°,然后分别在Rt△CDH和Rt△BDH中,利用三角函数的知识即可求得答案.
解答: 解:(1)如图:
解:(1)如图:
∵∠EAB=30°,∠FBC=30°,AE∥BF,
∴∠ABF=∠EAB=30°,
∴∠ABC=∠ABF+∠FBC=60°,
∵∠BAC=90°-∠EAB=60°,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=30海里,
在Rt△ACD中,∠DAC=90°-∠EAD=90°-60°=30°,
∴CD=AC•tan30°=10
(海里);
∵半小时后达到D处,
∴船航行的速度为:10
÷
=20
(海里/时);
 (2)过点D作DH⊥BC于点H,
(2)过点D作DH⊥BC于点H,
∵∠FBD=75°,∠FBC=30°,
∴∠DBH=45°,
∵BF∥CD,
∴∠DCH=∠FBC=30°,
在Rt△CDH中,DH=CD•tan30°=10
×
=10(海里),
在Rt△BDH中,∠DBH=45°,
∴BD=
=10
(海里).
 解:(1)如图:
解:(1)如图:∵∠EAB=30°,∠FBC=30°,AE∥BF,
∴∠ABF=∠EAB=30°,
∴∠ABC=∠ABF+∠FBC=60°,
∵∠BAC=90°-∠EAB=60°,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=30海里,
在Rt△ACD中,∠DAC=90°-∠EAD=90°-60°=30°,
∴CD=AC•tan30°=10
| 3 |
∵半小时后达到D处,
∴船航行的速度为:10
| 3 |
| 1 |
| 2 |
| 3 |
 (2)过点D作DH⊥BC于点H,
(2)过点D作DH⊥BC于点H,∵∠FBD=75°,∠FBC=30°,
∴∠DBH=45°,
∵BF∥CD,
∴∠DCH=∠FBC=30°,
在Rt△CDH中,DH=CD•tan30°=10
| 3 |
| ||
| 3 |
在Rt△BDH中,∠DBH=45°,
∴BD=
| DH |
| sin45° |
| 2 |
点评:此题考查了方向角问题.此题难度适中,注意掌握数形结合思想的应用,注意能构造直角三角形并能借助于解直角三角形的知识求解是解此题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,已知AC⊥CB,D、E分别为AC、CB的中点,且CD=CE=15,则△BEG的面积为( )
如图,已知AC⊥CB,D、E分别为AC、CB的中点,且CD=CE=15,则△BEG的面积为( )| A、50 | B、60 | C、75 | D、90 |
下列是几个汽车的标志,其中是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
[x]表示不大于x的最大整数,如[3.5]=3,[-2.7]=-3,[4]=4,…,则
的结果是( )
[
| ||||||
| 1005 |
| A、1005 | B、1004 |
| C、2010 | D、2009 |
 已知抛物线y=x2+bx+c,若抛物线经过点(1,-6),(-1,0)
已知抛物线y=x2+bx+c,若抛物线经过点(1,-6),(-1,0)